K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
24 tháng 5 2023
=>4a^2-5ab+b^2=0
=>(a-b)(4a-b)=0
=>a=b hoặc b=4a(loại)
=>P=b^2/3b^2=1/3
DN
2
26 tháng 9 2021
Ta có:
\(4a^2+b^2=5ab\Leftrightarrow4a^2+b^2-4ab-ab=0\)
\(\Leftrightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Leftrightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a-b=0\\4a-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=b\left(ktm\right)\\4a=b\left(tm\right)\end{matrix}\right.\)
\(\Rightarrow4a=b\)
\(\Rightarrow\dfrac{5ab}{3a^2+2b^2}=\dfrac{5a.4a}{3a^2+2.\left(4a\right)^2}=\dfrac{20a^2}{3a^2+32a^2}\)
\(=\dfrac{20a^2}{35a^2}=\dfrac{4}{7}\)
26 tháng 9 2021
\(4a^2+b^2=5ab\)
\(\Rightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)
\(\Rightarrow\left(a-b\right)\left(4a-b\right)=0\)
\(\Rightarrow b=4a\left(do.a\ne b\right)\)
\(\dfrac{5ab}{3a^2+2b^2}=\dfrac{20a^2}{3a^2+32a^2}=\dfrac{4}{7}\)
MN
1
PH
0
28 tháng 7 2021
a,\(5ab-45a^3b\)
=\(5ab\left(1-9a^2\right)\)
=\(5ab\left(1-3a\right)\left(1+3a\right)\)
b,\(3a-6ab+5-10b\)
=\(\left(3a-6ab\right)+\left(5-10b\right)\)
=\(3a\left(1-2b\right)+5\left(1-2b\right)\)
=\(\left(1-2b\right)\left(3a+5\right)\)
c,\(a^2-7ab-2a+14b\)
=\(\left(a^2-7ab\right)-\left(2a-14b\right)\)
=\(a\left(a-7b\right)-2\left(a-7b\right)\)
=\(\left(a-7b\right)\left(a-2\right)\)
d,\(4a^2-8b+4a-8ab\)
=\(\left(4a^2-8ab\right)+\left(4a-8b\right)\)
=\(4a\left(a-2b\right)+4\left(a-2b\right)\)
=\(\left(a-2b\right)\left(4a+4\right)\)
=\(4\left(a-2b\right)\left(a+1\right)\)
e,\(a^2-5a+15b-9b^2\)
=\(\left(a^2-9b^2\right)-\left(5a-15b\right)\)
=\(\left(a-3b\right)\left(a+3b\right)-5\left(a-3b\right)\)
=\(\left(a-3b\right)\left(a+3b-5\right)\)
2 tháng 10 2021
Bài 1:
a: \(4a^2-6b=2\left(2a^2-3b\right)\)
b: \(m^3n-2m^2n^2-mn\)
\(=mn\left(m^2-2mn-1\right)\)
2 tháng 10 2021
Bài 1:
a) \(4a^2-6b=2\left(a^2-3b\right)\)
b) \(=mn\left(m^2-2mn-1\right)\)
Bài 2:
a) \(=4\left(u-2\right)^2+v\left(u-2\right)=\left(u-2\right)\left(4u-8+v\right)\)
b) \(=a\left(a-b\right)^3-b\left(a-b\right)^2-b^2\left(a-b\right)=\left(a-b\right)\left[a\left(a-b\right)^2-b\left(a-b\right)-b^2\right]=\left(a-b\right)\left(a^3-2a^2b+ab^2-ab+b^2-b^2\right)=\left(a-b\right)\left(a^3-2a^2b+ab^2-ab\right)\)
TV
1
23 tháng 12 2020
Ta có: a+b+c=0
nên a+b=-c
Ta có: \(a^2-b^2-c^2\)
\(=a^2-\left(b^2+c^2\right)\)
\(=a^2-\left[\left(b+c\right)^2-2bc\right]\)
\(=a^2-\left(b+c\right)^2+2bc\)
\(=\left(a-b-c\right)\left(a+b+c\right)+2bc\)
\(=2bc\)
Ta có: \(b^2-c^2-a^2\)
\(=b^2-\left(c^2+a^2\right)\)
\(=b^2-\left[\left(c+a\right)^2-2ca\right]\)
\(=b^2-\left(c+a\right)^2+2ca\)
\(=\left(b-c-a\right)\left(b+c+a\right)+2ca\)
\(=2ac\)
Ta có: \(c^2-a^2-b^2\)
\(=c^2-\left(a^2+b^2\right)\)
\(=c^2-\left[\left(a+b\right)^2-2ab\right]\)
\(=c^2-\left(a+b\right)^2+2ab\)
\(=\left(c-a-b\right)\left(c+a+b\right)+2ab\)
\(=2ab\)
Ta có: \(M=\dfrac{a^2}{a^2-b^2-c^2}+\dfrac{b^2}{b^2-c^2-a^2}+\dfrac{c^2}{c^2-a^2-b^2}\)
\(=\dfrac{a^2}{2bc}+\dfrac{b^2}{2ac}+\dfrac{c^2}{2ab}\)
\(=\dfrac{a^3+b^3+c^3}{2abc}\)
Ta có: \(a^3+b^3+c^3\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ca-cb+c^2\right)-3ab\left(a+b\right)\)
\(=-3ab\left(a+b\right)\)
Thay \(a^3+b^3+c^3=-3ab\left(a+b\right)\) vào biểu thức \(=\dfrac{a^3+b^3+c^3}{2abc}\), ta được:
\(M=\dfrac{-3ab\left(a+b\right)}{2abc}=\dfrac{-3\left(a+b\right)}{2c}\)
\(=\dfrac{-3\cdot\left(-c\right)}{2c}=\dfrac{3c}{2c}=\dfrac{3}{2}\)
Vậy: \(M=\dfrac{3}{2}\)
15 tháng 7 2021
`a)x^4+2x^2y+y^2`
`=(x^2+y)^2`
`b)(2a+b)^2-(2b+a)^2`
`=(2a+b-2b-a)(2a+b+2b+a)`
`=(a-b)(3a+3b)`
`=3(a-b)(a+b)`
`c)8a^3-27b^3-2a(4a^2-9b^2)`
`=(2a-3b)(4a^2+6ab+9b^2)-2a(2a-3b)(2a+3b)`
`=(2a-3b)(4a^2+6ab+9b^2-3a^2-6ab)`
`=9b^2(2a-3b)`
16 tháng 7 2021
a) Ta có: \(x^4+2x^2y+y^2\)
\(=\left(x^2\right)^2+2\cdot x^2\cdot y+y^2\)
\(=\left(x^2+y\right)^2\)
b) Ta có: \(\left(2a+b\right)^2-\left(2b+a\right)^2\)
\(=\left(2a+b-2b-a\right)\left(2a+b+2b+a\right)\)
\(=\left(a-b\right)\left(3a+3b\right)\)
\(=3\left(a+b\right)\left(a-b\right)\)
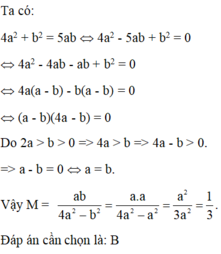
ta có: \(4a^2+b^2=5ab< =>4a^2-5ab+b^2=0< =>4a^2-4ab-ab+b^2=0< =>4a\left(a-b\right)-b\left(a-b\right)=0< =>\left(a-b\right)\left(4a-b\right)=0\)
do 2a>b>0=>4a>b>0=> 4a-b khác 0
=> a-b=0<=>a=b
P=\(\dfrac{ab}{4a^2-b^2}=\dfrac{ab}{\left(2a-b\right)\left(2a+b\right)}=\dfrac{ab}{\left(2a-a\right)\left(2a+a\right)}=\dfrac{a^2}{3a^2}=\dfrac{1}{3}\)
vậy............
chúc bạn hcoj tốt ^^