Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì tổng của 5 số bất ki là 1 số dương nên chắc chắn trong 31 số nguyên, có 1 số dương.
Vậy số các số nguyên còn lại là: 31-1=30 (số)
Ta chia 30 số này ra thành 6 nhóm, mỗi nhóm gồm 5 số. Mà ta có tổng của 5 số bất kì là 1 số dương nên tổng của 6 nhóm mà mỗi nhóm đều là số dương sẽ là 1 số dương. Vậy tổng của 30 số nguyên là một số dương.
Ta có: Tổng của 30 số nguyên là 1 số dương và 1.số nguyên còn lại là số dương nên Tổng 31 số là số dương.=>đpcm.

Bài 1:
a) Gọi số liền sau là a+1. Vì a dương (a<0) nên số liền sau a hơn a 1 đơn vị nên cũng là số dương.=>đpcm.
b) Ta có:Nếu a âm thì a<0. Số liền trước a nhỏ hơn a nên cũng là số âm.
c) Vậy ta có thể kết luận: Số liền trước của 1 số dương chua chắc là số dương ( Trường hợp a=1, số liền trước a là 0, không phải số dương). Số liền sau của một số âm chưa chắc là số âm ( Trường hợp a=-1 thì số liền sau a là 0 và không là số âm).

Số các số nguyên dương thỏa mãn bài toán lập thành một cấp số cộng với số hạng đầu u 1 = 3 và công sai d = 3
Do đó ![]()
Chọn C.

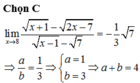
Trong các số đã cho ít nhất có 1 số dương vì nếu trái lại tất cả đều là số âm thì tổng của 5 số bất kỳ trong chúng sẽ là số âm trái với giả thiết.
Tách riêng số dương đó còn 30 số chi làm 6 nhóm. Theo đề bài tổng các số của mỗi nhóm đều là số dương nên tổng của 6 nhóm đều là số dương và do đó tổng của 31 số đã cho đều là số dương.
Vì tổng của 5 số bất kì là một số nguyên dương nên trong 31 số phải có ít nhất 1 số nguyên dương.
Vậy số các nguyên còn lại là: 31-1=30 (số nguyên)
Ta chia 30 số nguyên này ra thành 6 nhóm, mỗi nhóm gồm 5 số nguyên. Theo đề bài, ta có tổng của 5 số nguyên bất kì là 1 số nguyên dương, vậy tổng của 6 nhóm mà mỗi nhóm có 5 số nguyên là 1 số dương => 30 số nguyên còn lại là số dương.
Vì tổng của 30 số hạng là 1 số nguyên dương, mà số còn lại cũng là số nguyên dương nên tổng 31 số là số nguyên dương => đpcm.