Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Để hệ 3 điện tích cân bằng thì lực điện do 2 điện tích bất kì tác dụng lên điện tích còn lại phải bằng 0



a) Tìm lực tương tác tĩnh diện giữa hai điện tích.
- Lực tương tác giữa hai điện tích là:
F = k q 1 . q 2 r 2 = 9.10 9 . 10 − 8 . − 2.10 − 8 0 , 1 2 = 1 , 8.10 − 4 N .
b) Muốn lực hút giữa chúng là 7 , 2 . 10 - 4 N. Tính khoảng cách giữa chúng:
Vì lực F tỉ lệ nghịch với bình phương khoảng cách nên khi F ' = 7 , 2 . 10 - 4 N = 4 F ( tăng lên 4 lần) thì khoảng cách r giảm 2 lần: r ' = r 2 = 0 , 1 2 = 0,05 (m) =5 (cm).
Hoặc dùng công thức:
F ' = k q 1 . q 2 r 2 ⇒ r = k q 1 . q 2 F ' = 9.10 9 10 − 8 .2.10 − 8 7 , 2.10 − 4 = 0,05 (m) = 5 (cm).
c) Thay q 2 bởi điện tích điểm q 3 cũng đặt tại B như câu b thì lực lực đẩy giữa chúng bây giờ là 3 , 6 . 10 - 4 N . Tìm q 3 ?
F = k q 1 . q 3 r 2 = > q 3 = F . r 2 k q 1 = 3 , 6.10 − 4 .0 , 1 2 9.10 9 .10 − 8 = 4.10 − 8 C .
Vì lực đẩy nên q 3 cùng dấu q 1 .
d) Tính lực tương tác tĩnh điện giữa q 1 và q 3 như trong câu c (chúng đặt cách nhau 10 cm) trong chất parafin có hằng số điện môi ε = 2 .
Ta có: lực F tỉ lệ nghịch với ε nên F ' = F ε = 3 , 6.10 − 4 2 = 1 , 8 . 10 - 4 ( N ) .
Hoặc dùng công thức: F ' = k q 1 . q 3 ε r 2 = 9.10 9 10 − 8 .4.10 − 8 2.0 , 1 2 = 1 , 8 . 10 - 4 ( N ) .


Để hệ 3 điện tích cân bằng thì lực điện tác dụng lên 2 điện tích bắt kì tác dụng lên điện tích còn lại phải bằng 0.
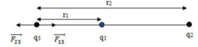
Để q3 cân bằng thì F23=F13 = \(\dfrac{k\left|q_1q_3\right|}{r^2_{1^{ }}}=\dfrac{k\left|q_2q_3\right|}{r^2_2}\left(1\right)\)
=> Điện tích q3 mang dấu âm, nằm ngoài khoảng q1,q2 và gần q1 hơn (Vì nằm gần vị trí điện tích có độ lớn lớn hơn)
Từ (1) => \(\dfrac{r1}{r2}=\sqrt{\dfrac{q1}{q2}}=\dfrac{1}{3}\)
Có: r2 - r1 =12 => r1=6 cm, r2=18 cm.
Để q1 cân bằng thì F31 = F21 khai triển và thay số ta được : q3 = -4,5.10-8 C.

Các điện tích q 1 v à q 2 tác dụng lên điện tích q3 các lực F 1 → và F 2 → có phương chiều như hình vẽ:
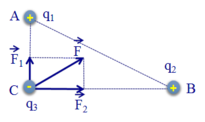
Có độ lớn: F 1 = k | q 1 q 3 | A C 2 = 9 . 10 9 | 27.10 − 8 . ( − 10 − 7 ) | 0 , 3 2 = 27 . 10 - 4 (N).
F 2 = k | q 2 q 3 | B C 2 = 9 . 10 9 | 64.10 − 8 . ( − 10 − 7 ) | 0 , 4 2 = 36 . 10 - 4 (N).
Lực tổng hợp do q 1 v à q 2 tác dụng lên q 3 là:
F → = F 1 → + F 2 → ; có phương chiều như hình vẽ, có độ lớn: F = F 1 2 + F 2 2 = 45 . 10 - 4 N.

a. Xác định lực khi cho q1, q2 tác dụng lên q3
Hợp lực tác dụng lên q3:
\(\vec{F_3}=\vec{F_{13}}+\vec{F_{23}}\)
Suy ra độ lớn:
\(F_3=F_{23}-F_{13}\) (1)
\(F_{13}=9.10^9.\dfrac{|q_1.q_3|}{AC^2}=9.10^9.\dfrac{|6.10^{-9}.2.10^{-9}|}{0,06^2}=3.10^{-5}N\)
\(F_{23}=9.10^9.\dfrac{|q_2.q_3|}{BC^2}=9.10^9.\dfrac{|3.10^{-9}.2.10^{-9}|}{0,03^2}=6.10^{-5}N\)
Thay vào (1) ta tìm được \(F_3=3.10^{-5}(N)\)
b. Ý này tương tự bạn nhé, phân tích lực --> Tổng hợp lực --> Rút ra biểu thức độ lớn --> Thay số.
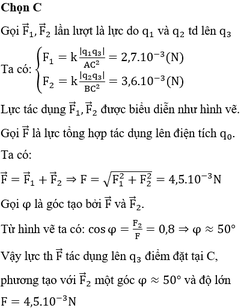
giúp mình với