Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) vì \(q_1\) và \(q_2\) trái dấu nên \(q_3\) không thể đặc ở giữa \(AB\) và cũng không thể nằm ngoài giá của \(\overrightarrow{AB}\) vì khi đó tổng các lực tác dụng lên \(q_3\) sẽ khác không .
theo định luật \(Cu-lông\) ta có :
\(F_{13}=\dfrac{k.\left|q_1q_3\right|}{\varepsilon AC^2}=\dfrac{k\left|2.10^{-8}q_3\right|}{\varepsilon AC^2}\) ; \(F_{23}=\dfrac{k\left|q_2q_3\right|}{\varepsilon BC^2}=\dfrac{k\left|-8.10^{-8}q_3\right|}{\varepsilon BC^2}=\dfrac{k\left|8.10^{-8}q_3\right|}{\varepsilon BC^2}\)
\(\)để \(q_3\) cân bằng thì \(F_{13}=F_{23}\Leftrightarrow\dfrac{k\left|2.10^{-8}q_3\right|}{\varepsilon AC^2}=\dfrac{k\left|8.10^{-8}q_3\right|}{\varepsilon BC^2}\)
\(\Leftrightarrow\dfrac{AC^2}{BC^2}=\dfrac{2.10^{-8}}{8.10^{-8}}=\dfrac{1}{4}\Leftrightarrow\dfrac{AC}{BC}=\dfrac{1}{2}\Leftrightarrow BC=2AC\)
\(\Rightarrow A\) là trung điểm của \(BC\) với đoạn \(AB=8cm\) .
b) theo nhận xét ta thấy \(q_3< 0\) vì nếu \(q_3>0\) thì \(F_{31}\) cùng hướng với \(F_{21}\) nên \(q_1\) không thể nào cân bằng
để \(q_1\) và \(q_2\) cần bằng thì : \(\left\{{}\begin{matrix}F_{31}=F_{21}\\F_{32}=F_{12}\end{matrix}\right.\Leftrightarrow F_{31}=F_{21}=F_{32}\)
nên ta chỉ cần \(F_{31}=F_{21}\) là đủ
\(\Rightarrow\dfrac{K\left|q_3q_1\right|}{\varepsilon AC^2}=\dfrac{k\left|q_2q_1\right|}{\varepsilon AB^2}\Leftrightarrow\dfrac{k\left|q_3q_1\right|}{\varepsilon8^2}=\dfrac{k\left|q_2q_1\right|}{\varepsilon8^2}\Leftrightarrow\left|q_3\right|=\left|q_2\right|\)
\(\Leftrightarrow\left|q_3\right|=\left|-8.10^{-8}\right|=8.10^{-8}\Leftrightarrow q_3=\pm8.10^{-8}\)
mà \(q_3< 0\Rightarrow q_3=-8.10^{-8}\)
vậy \(q_3=-8.10^{-8}\)

1)lực tĩnh điện đẩy nhau cảu A và B là :
9*10^(9)*((1.8*10^(-8)*5.4*10^(-9))/0.03^(2))=9.72*10^(-4) N
gọi X là q c
vì tổng lục tĩnh điện tác dụng lên A ss with BC nên
ta có pt
9.72*10^(-4)+(9*10^(9)*((1.8*10^(-8)*X)/0.04^(2))=9*10^(9)*((5.4*10^(-9)*X)/0.056(2))
giải tìm được X=-1.8*10^(-8)
không chắc đúng đâu !
hình như sai cái gì đó chổ pt thay 0.05^(2) =>0.5^(2)
ta được X=-9.6*10^(-9)

a/
+ + A B + C q1 q2 q3 F F F 23 13 hl → → →
Ta có: \(\vec{F_{hl}}=\vec{F_{13}}+\vec{F_{23}}\)
Do \(\vec{F_{13}}\uparrow\downarrow\vec{F_{23}}\) nên: \(F_{hl}=\left|F_{13}-F_{23}\right|\) (1)
\(F_{13}=9.10^9\frac{\left|q_1q_2\right|}{AC^2}=0,045N\)
\(F_{23}=9.10^9\frac{\left|q_1q_2\right|}{BC^2}=0,01N\)
Thay vào (1) ta được \(F_{hl}=0,035N\)
b/
+ + + A B D q1 q2 q3 F F F 23 13 hl → → →
Hợp lực: \(\vec{F_{hl}}=\vec{F_{13}}+\vec{F_{23}}\)
Do hai lực cùng phương cùng chiều nên độ lớn:
\(F_{hl}=F_{13}+F_{23}\)(2)
\(F_{13}=9.10^9.\frac{\left|q_1q_3\right|}{AD^2}=7,2.10^{-3}N\)
\(F_{23}=9.10^9.\frac{\left|q_2q_3\right|}{BD^2}=0,9.10^{-3}N\)
Thế vào (2) ta được \(F_{hl}=8,1.10^{-3}N\)

Hai điện tích đẩy nhau => q1 và q2 cùng dấu
q1 + q2 = – 6.10-6 C (1) => |q1q2| = q1q2
F = 1,8 N; |q1| > |q2|; r = 20cm = 20.10-2m; ε = 1
\(F=9.10^9.\frac{\left|q_1q_2\right|}{r^2}\Rightarrow\left|q_1q_2\right|=8.10^{-12}\) (2)
Từ (1) và (2) => q1 = – 4.10-6 C; q2 = – 2.10-6 C.

Bài làm.
Điện tích điểm q1 = 3.10-8 C đặt tại điểm A, q2 = - 4.10-8 C đặt tại điểm B, AB = 10cm.
Gọi C là điểmmà tại đó cường độ điện trường bằng không.
Gọi −−→E1CE1C→ và −−→E2CE2C→ là cường độ điện trường của q1 và q2 tại C.
Tại đó −−→E1CE1C→ = - −−→E2CE2C→. Hai vectơ này phải cùng phương, tức là điểm C phải nằm trên đường thẳng AB (Hình 3.3).
Hai vectơ này phải ngược chiều, tức là phải nằm ngoài đoan AB. Vì hai vectơ này phải có môđun bằng nhau, tức là điểm C gần A hơn B vì |q1| < |q2|.
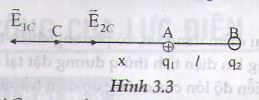
Đặt AN = l, AC = x, ta có :
k.|q1|ε.x2=k.|q2|ε.(l+x)2k.|q1|ε.x2=k.|q2|ε.(l+x)2 hay (l+xx)2=∣∣q2q1∣∣=43(l+xx)2=|q2q1|=43 hay x = 64,6cm.
Ngoài ra còn phải kể tất cả các điểm nằm rất xa q1 và q2. Tại điểm C và các điểm này thì cường độ điện trường bằng không, tức là không có điện trường
Để hệ 3 điện tích cân bằng thì lực điện tác dụng lên 2 điện tích bắt kì tác dụng lên điện tích còn lại phải bằng 0.
Để q3 cân bằng thì F23=F13 = \(\dfrac{k\left|q_1q_3\right|}{r^2_{1^{ }}}=\dfrac{k\left|q_2q_3\right|}{r^2_2}\left(1\right)\)
=> Điện tích q3 mang dấu âm, nằm ngoài khoảng q1,q2 và gần q1 hơn (Vì nằm gần vị trí điện tích có độ lớn lớn hơn)
Từ (1) => \(\dfrac{r1}{r2}=\sqrt{\dfrac{q1}{q2}}=\dfrac{1}{3}\)
Có: r2 - r1 =12 => r1=6 cm, r2=18 cm.
Để q1 cân bằng thì F31 = F21 khai triển và thay số ta được : q3 = -4,5.10-8 C.