Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) đây nha : https://hoc24.vn/hoi-dap/question/637285.html
câu 2 cũng chả khác gì cả

TenAnh1
TenAnh1
A = (-4, -6.26)
A = (-4, -6.26)
A = (-4, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
B = (11.36, -6.26)
Do \(\overrightarrow{NP}=\overrightarrow{DC}\); \(\overrightarrow{AM}=\overrightarrow{BA}\Rightarrow\overrightarrow{MA}=\overrightarrow{AB}\).
Do tứ giác ABCD là hình bình hành nên \(\overrightarrow{AB}=\overrightarrow{DC}\).
Vì vậy \(\overrightarrow{NP}=\overrightarrow{MA}\) nên tứ giác NPAM là hình bình hành.
Vì vậy \(\overrightarrow{PA}=\overrightarrow{NM}\). (1)
Mà \(\overrightarrow{MN}=\overrightarrow{DA}\) suy ra \(\overrightarrow{NM}=\overrightarrow{AD}\) . (2)
Mặt khác \(\overrightarrow{AD}=\overrightarrow{BC}\) (do tứ giác ABCD là hình bình hành). (3)
Từ (1);(2);(3) suy ra:\(\overrightarrow{PA}=\overrightarrow{BC}\).
Mà \(\overrightarrow{PQ}=\overrightarrow{BC}\Rightarrow\overrightarrow{PQ}=\overrightarrow{PA}\).
Vì vậy hai điểm A và Q trùng nhau nên \(\overrightarrow{AQ}=\overrightarrow{0}\).

Gọi O là tâm bình hành
\(\overrightarrow{MA}+2\overrightarrow{MB}+2\overrightarrow{MC}+\overrightarrow{MD}=\overrightarrow{0}\Leftrightarrow6\overrightarrow{MO}+\overrightarrow{OA}+2\overrightarrow{OB}+2\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}\)
Dễ dàng nhìn ra trong hình bình hành ABCD tâm O thì: \(\hept{\begin{cases}\overrightarrow{OA}+\overrightarrow{OD}=-\frac{1}{2}\overrightarrow{AB}\\\overrightarrow{OB}+\overrightarrow{OD}=\frac{1}{2}\overrightarrow{AB}\end{cases}}\)--->thế lên trên:
\(\Rightarrow6\overrightarrow{MO}-\frac{1}{2}\overrightarrow{AB}+\overrightarrow{AB}=\overrightarrow{0}\Leftrightarrow\overrightarrow{OM}=\frac{1}{12}\overrightarrow{AB}\)---> Dễ dàng có được M là điểm cố định (Vì các điểm O,A,B đều cố định)
Vậy điểm M được xác định bằng cách lấy đường thẳng qua O song song AB rồi trong nửa mặt phẳng bờ là BD có chứa điểm C ta lấy điểm M thuộc đường thẳng vừa dựng được sao cho đoạn OM có độ dài đúng bằng 1/12 độ dài AB.
Gọi O là giao điểm hai đoạn thẳng AC và BD.
Dựng điểm M như sau:
Trên nửa mặt phẳng bờ AC phía B, vẽ tia Ot song song AB.
Trên tia này, Bạn lấy điểm M cách O một đoạn bằng MỘT PHẦN SÁU AB.
Đó là điểm cần tìm.

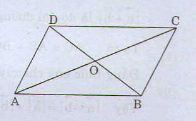
A B C D O
a) \(\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO}=\left(\overrightarrow{AO}+\overrightarrow{CO}\right)+\left(\overrightarrow{BO}+\overrightarrow{DO}\right)\)
\(=\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\).
b) \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}=\overrightarrow{AC}+\overrightarrow{AC}=2\overrightarrow{AC}\).
c) \(\overrightarrow{OC}-\overrightarrow{OD}=\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{DC}\).
\(\overrightarrow{CC'}=\overrightarrow{CB}+\overrightarrow{BB'}+\overrightarrow{B'C'}=\overrightarrow{BB'}+\overrightarrow{DA}+\overrightarrow{AD'}=\overrightarrow{BB'}+\overrightarrow{DD'}\)
\(\Rightarrow\overrightarrow{CC}'=-\overrightarrow{B'B}-\overrightarrow{D'D}\)
\(\Rightarrow\overrightarrow{B'B}+\overrightarrow{CC'}+\overrightarrow{D'D}=\overrightarrow{B'B}-\overrightarrow{B'B}-\overrightarrow{D'D}+\overrightarrow{D'D}=\overrightarrow{0}\)