Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: `\hat(tOz)` và `\hat(t'Oz')` là 2 góc đối đỉnh.
`=> \hat(tOz) = \hat(t'Oz)`
Mà `\hat(tOz) + \hat(t'Oz) = 110^o`
`<=> \hat(tOz) = \hat(t'Oz) = 110^o : 2 =55^o`
`=> \hat(t'Oz)=\hat(tOz') = 180^o - 55^o=125^o`
vì \(\angle\left(tOz\right)=\angle\left(t'Oz'\right)\)(đối đỉnh)
\(=>\angle\left(tOz\right)+\angle\left(t'Oz'\right)=110< =>\angle\left(tOz\right)=\angle\left(t'Oz'\right)=\dfrac{110}{2}=55^o\)
\(=>\angle\left(tOz'\right)=\angle\left(t'Oz\right)=180-55=125^o\)

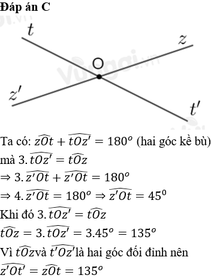
Ta có hình vẽ:
Ta có: góc tOz = góc t'Oz' (đđ)
Mà góc tOz + góc t'Oz' = 1100
hay góc tOz + góc tOz = 1100 (góc tOz = góc t'Oz')
=> 2.góc tOz = 1100
=> góc tOz = 1100 / 2 = 550
Ta có: góc tOz + góc zOt' = 1800 (kb)
=> góc 550 + góc zOt' = 1800
=> góc zOt' = 1800 - 550 = 1250
Ta có: góc tOz = góc t'Oz' = 550 (đđ)
Ta có: góc zOt' = góc z'Ot = 1250 (đđ).

B1: \(\widehat{yOx'}=180^o-45^o=135^o\)(2 góc kề bù)
\(\widehat{x'Oy'}=45^o\)(đối đỉnh với góc xOy)
\(\widehat{xOy'}=135^o\)(đói đỉnh với góc yOx')
B2: Ta có: Ot và Ot' đối nhau => \(\widehat{tOt'}=180^o\)=>\(\widehat{tOz}=\frac{\widehat{tOt'}}{5}=\frac{180^o}{5}=36^o\)=> \(\widehat{t'Oz}=36^o\)(đối đỉnh với \(\widehat{tOz}\))

a) Các cặp góc kề bù
\(\widehat{xOy}\) và \(\widehat{yOx'}\)
\(\widehat{yOx'}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy'}\) và \(\widehat{xOy'}\)
\(\widehat{xOy'}\) và \(\widehat{xOy}\)
Các cặp góc đối:
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{y'Ox}\)
b) Do \(\widehat{xOy}\) kề bù với \(\widehat{xOy'}\)
\(\Rightarrow\widehat{xOy}+\widehat{xOy'}=180^o\)
\(\Rightarrow\widehat{xOy'}=180^o-70^o=110^o\)
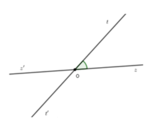
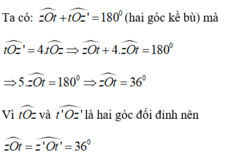

hình vẽ bạn ơi
Ta có: \(\widehat{tOz'}+\widehat{tOz}=180^0\)(hai góc kề bù)
\(\Leftrightarrow5\cdot\widehat{tOz}=180^0\)
\(\Leftrightarrow\widehat{tOz}=36^0\)
\(\Leftrightarrow\widehat{tOz'}=144^0\)
\(\widehat{z'Ot'}=36^0\); \(\widehat{zOt'}=144^0\)