Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
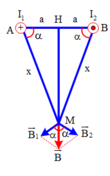
Gọi M là điểm mà tại đó cảm ứng từ tổng hợp bằng 0.
Ta có: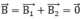 
Suy ra: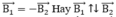 
và B1 = B2
Do đó tập hợp những điểm M cần tìm phải nằm trên mặt phẳng chứa hai dây dẫn I1 và I2.
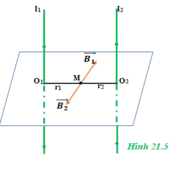
Từ hình 21.5:
+ Nếu M nằm ngoài khoảng cách giữa dây (1) và dây (2) thì: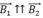 
⇒ loại.
+ Nếu M nằm giữa khoảng cách dây (1) và dây (2) thì: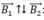 
nhận trường hợp này.
Do I1 > I2 nên điểm M nằm gần dây (2) hơn.
Ta có: r1 + r2 = 50cm (∗)
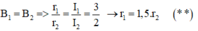
Thay (∗∗) vào (∗) ta tìm được r1 = 30cm và r2 = 20cm
Vậy: tập hợp những điểm M có B = 0 là đường thẳng thuộc mặt phẳng chứa dây (1) và dây (2), nằm giữa dây (1) và dây (2), cách dây I1 30cm, dây I2 20cm
Đáp án: cách dây thứ nhất 30cm
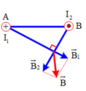
Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi vào tại B. Tam giác AMB vuông tại M. Các dòng điện I1 và I2 gây ra tại M các vectơ cảm ứng từ B 1 → v à B 2 → có phương chiều như hình vẽ, có độ lớn:
a)Hai dây dẫn cùng chiều.
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{5}{0,05}=2\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{1}{0,05}=4\cdot10^{-6}T\)
\(B=B_1+B_2=2\cdot10^{-5}+4\cdot10^{-6}=2,4\cdot10^{-5}T\)
b)Hai dây dẫn ngược chiều nhau.
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{5}{0,05}=2\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{1}{0,15}=1,33\cdot10^{-6}T\)
\(B=\left|B_1-B_2\right|=\left|2\cdot10^{-5}-1,33\cdot10^{-6}\right|=1,867\cdot10^{-5}T\)
c)Hai dây dẫn vuông góc nhau (vì \(\sqrt{6^2+8^2}=10\))
\(B_1=2\cdot10^{-7}\cdot\dfrac{I_1}{r_1}=2\cdot10^{-7}\cdot\dfrac{5}{0,06}=1,67\cdot10^{-5}T\)
\(B_2=2\cdot10^{-7}\cdot\dfrac{I_2}{r_2}=2\cdot10^{-7}\cdot\dfrac{1}{0,08}=2,5\cdot10^{-6}T\)
\(B=\sqrt{B_1^2+B_2^2}=\sqrt{\left(1,67\cdot10^{-5}\right)^2+\left(2,5\cdot10^{-6}\right)^2}=1,688\cdot10^{-5}T\)
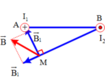
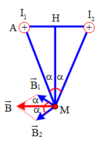
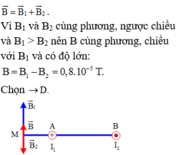
Ta có: `B_1 =B_2`
Vì `I_1 ;I_2` cùng chiều.
`=>B_[\text{tại tđ}]=|B_1 -B_2|=0 (T)`