Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét d là đường thẳng đi qua ít nhất 3 điểm trong 100 điểm. Giả sử có nhiều hơn 1 điểm nằm ngoài d. Xét 2 điểm A, B nằm ngoài d và 2 điểm C, D thuộc d và C, D không thuộc AB. Khi đó 4 điểm A, B, C, D không thỏa mãn đầu bài. Vậy có nhiều nhất 1 điểm nằm ngoài d. Bỏ điểm đó đi ta có 99 điểm thẳng hàng

Trên mặt phẳng cho n > = điểm sao cho khoảng cách giữa 2 điểm bất kì đôi một khác nhau. Người ta nối mỗi điểm với điểm gần nhất.
CMR qua mỗi điểm co không quá 5 đoạn thẳng

Đề bài thiếu : không có 4 điểm nào cùng thuộc 1 đường tròn ( nhỡ n điểm này cùng thuộc 1 đường tròn)
Có n điểm mà ko có 3 điểm nào thẳng hàng luôn tồn tại 2 điểm sao cho n−2 điểm còn lại ∈ cùng một nửa mặt phẳng có bờ là đường thẳng chứa đoạn thẳng có 2 mút là 2 điểm trên
gọi 2 điểm đó là A1,A2 và n−2 điểm còn lại là B1,B2,B3,...,Bn−2
Xét các góc A1BiA2ˆ(i=1,2,3,..,n−2)
luôn tồn tại một góc có số đo lớn hơn hẳn những góc còn lại giả sử là A1BmA2ˆ
khi đó vẽ đường tròn ngoại tiếp TG này
Dễ cm nếu ∃1 điểm nằm trong đường tròn đó gs là Bn thì A1BnA2ˆ>A1BmA2ˆ
=> vô lý vì góc trên là lớn nhất
P/s : Bài náy có thể mở rộng là có thể vẽ 1 đường tròn chứa đúng m điểm với (m≤n)
Trong các khoảng cách từ O đến các cạnh của đa giác, giả sử khoảng cách từ O đến cạnh AB là nhỏ nhất (đó là đường vuông góc OE)
Ta sẽ chứng minh E phải thuộc cạnh AB
Giả sử E nằm ngoài cạnh AB, khi đó OE phải cắt một trong các cạnh của đa giác tại G
Dễ thấy OF<OG<OE nghĩa là điểm O gần cạnh BC hơn cạnh AB
Điều này trái với việc chọn cạnh AB, từ đó ta có điều phải chứng minh
A B E G O F C D

Chỗ kia chắc là \(n\) điểm chứ không phải \(n+1\) đâu.
Giả sử \(n\) điểm đã cho không thẳng hàng. Gọi S là tập hợp gồm \(n\) điểm đã cho và \(T=\left\{\left(A,B,C\right):A,B,C\in S|d\left(A,BC\right)>0\right\}\).
Vì n điểm đã cho không thẳng hàng nên \(T\ne\varnothing\). Mà T là có hữu hạn phần tử nên tồn tại phần tử \(\left(A,B,C\right)\in T\) sao cho \(d\left(A,BC\right)\) nhỏ nhất.
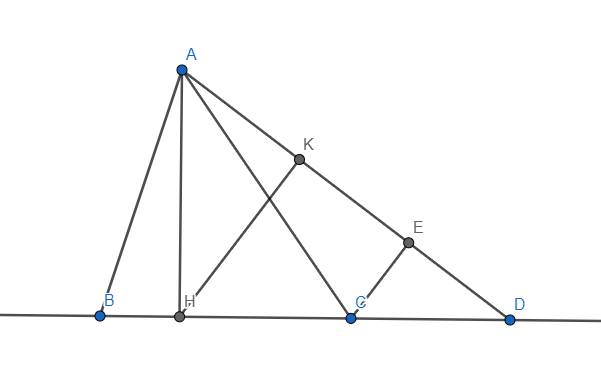
Theo giả thiết thì đường thẳng BC còn đi qua 1 điểm thứ ba nữa là \(D\in S\) . Không mất tính tổng quát, giả sử C nằm giữa B và D. Hạ \(AH\perp BC\), \(HK\perp AD\) và \(CE\perp AD\). Ta có \(CE< HK< AH\). Suy ra phần tử \(\left(C,A,D\right)\in T\) có \(d\left(C,AD\right)< d\left(A,BC\right)\), điều này là vô lí vì ta đã giả sử phần tử \(\left(A,B,C\right)\in T\) có \(d\left(A,BC\right)\) nhỏ nhất.
Vậy điều giả sử là sai, suy ra \(n\) điểm đã cho thẳng hàng.
Vẫn như lần trước nhé bạn. Nếu bạn không xem được câu trả lời trên đây thì vào trong trang cá nhân của mình xem nhé.
Xét d là đường thẳng đi qua ít nhất 3 điểm trong 100 điểm. Giả sử có nhiều hơn 1 điểm nằm ngoài d. Xét 2 điểm A, B nằm ngoài d và 2 điểm C, D thuộc d và C, D không thuộc AB. Khi đó 4 điểm A, B, C, D không thỏa mãn đầu bài. Vậy có nhiều nhất 1 điểm nằm ngoài d. Bỏ điểm đó đi ta có 99 điểm thẳng hàng
k mk nhé
mấy bài này mình thấy khó hiểu quá à