
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

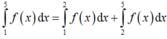
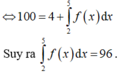

\(f\left(0\right)=\dfrac{b}{d}\Rightarrow f\left(f\left(0\right)\right)=0\Rightarrow f\left(\dfrac{b}{d}\right)=0\)
\(\Rightarrow\dfrac{\dfrac{ab}{d}+b}{\dfrac{cb}{d}+d}=0\Rightarrow b\left(a+d\right)=0\Rightarrow\left[{}\begin{matrix}b=0\\d=-a\end{matrix}\right.\)
TH1: \(b=0\)
\(f\left(1\right)=1\Rightarrow a=c+d\)
\(f\left(2\right)=2\Rightarrow2a=2\left(2c+d\right)\Rightarrow a=2c+d\)
\(\Rightarrow2c+d=c+d\Rightarrow c=0\) (ktm)
TH2: \(d=-a\)
\(f\left(1\right)=1\Rightarrow a+b=c+d=c-a\Rightarrow2a+b=c\) (1)
\(f\left(2\right)=2\Rightarrow2a+b=2\left(2c+d\right)=2\left(2c-a\right)\Rightarrow4a+b=4c\) (2)
Trừ (2) cho (1) \(\Rightarrow2a=3c\Rightarrow\dfrac{a}{c}=\dfrac{3}{2}\)
\(\Rightarrow\lim\limits_{x\rightarrow\infty}\dfrac{ax+b}{cx+d}=\dfrac{a}{c}=\dfrac{3}{2}\)
Hay \(y=\dfrac{3}{2}\) là tiệm cận ngang

Đáp án: C.
Vì lnC mới là số thực tùy ý, D sai vì không cộng hằng số C vào biến.

Đáp án: C.
Vì lnC mới là số thực tùy ý, D sai vì không cộng hằng số C vào biến.

Lời giải:
\(f'(x)=(x^2-1)(x+1)(5-x)=(x+1)^2(x-1)(5-x)\)
Ta thấy \((x-1)(5-x)\geq 0, \forall x\in [1;5]\Rightarrow f'(x)=(x+1)^2(x-1)(5-x)\geq x\in [1;5]\)
Lập bảng biến thiên ta thấy hàm số đồng biến trên đoạn $[1;5]$ do đó :
\(f(1)< f(2)< f(4)\)
Đáp án B
f'(x)>=0 x thuoc [1;5]
qua du kl f(x) dong bien
=>viec Lap bang thien la viec lam thua vo bo
dap khuon robot

\(y'=\frac{5\left(x^2+4\right)-2x.5x}{\left(x^2+4\right)}f'\left(\frac{5x}{x^2+4}\right)=\frac{5\left(4-x^2\right)}{x^2+4}f'\left(\frac{5x}{x^2+4}\right)\)
\(=\frac{5\left(2-x\right)\left(2+x\right)}{\left(x^2+4\right)}.\left(\frac{5x}{x^2+4}\right)^2.\left(\frac{5x}{x^2+4}-1\right)\left(\frac{65x}{x^2+4}-15\right)^3\)
\(=\frac{5\left(2-x\right)\left(2+x\right).25x^2\left(x-4\right)\left(1-x\right)\left(x-3\right)^3\left(4-3x\right)^3.5^3}{\left(x^2+4\right)^7}\)
Ta thấy \(y'=0\) có 7 nghiệm nhưng nghiệm \(x=0\) có mũ chẵn nên hàm số có 6 điểm cực trị

Lời giải:
\(a+b=3\Rightarrow a+(b-2)=1\Rightarrow b-2=1-a\)
Ta có:
\(f(x)=\frac{9^x}{9^x+3}\Rightarrow f(a)=\frac{9^a}{9^a+3}\) (1)
\(f(b-2)=f(1-a)=\frac{9^{1-a}}{9^{1-a}+3}=\frac{9}{9^a\left(\frac{9}{9^a}+3\right)}\)
\(=\frac{9}{9+3.9^a}=\frac{3}{3+9^a}\) (2)
Từ (1),(2) suy ra \(f(a)+f(b-2)=\frac{9^a}{9^a+3}+\frac{3}{3+9^a}=\frac{9^a+3}{9^a+3}=1\)
Đáp án A