K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
23 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
`a)`
\(5^x+5^{x+2}=650\)
`\Rightarrow 5^x + 5^x . 5^2 = 650`
`\Rightarrow 5^x . (1 + 5^2) = 650`
`\Rightarrow 5^x . 26 = 650`
`\Rightarrow 5^x = 650 \div 26`
`\Rightarrow 5^x = 25`
`\Rightarrow 5^x = 5^2`
`\Rightarrow x = 2`
Vậy, `x = 2`
`b)`
`(4x + 1)^2 = 25.9`
`\Rightarrow (4x + 1)^2 = 225`
`\Rightarrow (4x + 1)^2 = (+-15^2)`
`\Rightarrow`\(\left[{}\begin{matrix}4x-1=15\\4x-1=-15\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}4x=16\\4x=-14\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=4\\x=-\dfrac{7}{2}\end{matrix}\right.\)
Vậy, `x \in`\(\left\{-\dfrac{7}{2};4\right\}\)
`c)`
\(2^x+2^{x+3}=144\)
`\Rightarrow 2^x + 2^x . 2^3 = 144`
`\Rightarrow 2^x . (1 + 2^3) = 144`
`\Rightarrow 2^x . 9 = 144`
`\Rightarrow 2^x = 144 \div 9`
`\Rightarrow 2^x = 16`
`\Rightarrow 2^x = 2^4`
`\Rightarrow x = 4`
Vậy, `x = 4`
`d)`
\(3^{2x+2}=9^{x+3}\)
`\Rightarrow `\(3^{2x+2}=\left(3^2\right)^{x+3}\)
`\Rightarrow `\(3^{2x+2}=3^{2x+6}\)
`\Rightarrow 2x + 2 = 2x + 6`
`\Rightarrow 2x - 2x = 6 - 2`
`\Rightarrow 0 = 4 (\text {vô lý})`
Vậy, `x` không có giá trị nào thỏa mãn.
`e)`
\(x^{15}=x^2\)
`\Rightarrow `\(x^{15}-x^2=0\)
`\Rightarrow `\(x^2\cdot\left(x^{13}-1\right)=0\)
`\Rightarrow `\(\left[{}\begin{matrix}x^2=0\\x^{13}-1=0\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=0\\x^{13}=1\end{matrix}\right.\)
`\Rightarrow `\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy, `x \in`\(\left\{0;1\right\}.\)
AD
23 tháng 7 2023
\(a,5^x+5^{x+2}=650\\ \Rightarrow5^x+5^x.5^2=650\\ \Rightarrow5^x\left(1+5^2\right)=650\\ \Rightarrow5^x.26=650\\ \Rightarrow5^x=25\\ \Rightarrow5^x=5^2\\ \Rightarrow x=2\)
\(b,\left(4x+1\right)^2=25.9\\\Rightarrow\left(4x+1\right)^2=225\\ \Rightarrow\left[{}\begin{matrix}4x+1=15\\4x+1=-15\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=\dfrac{7}{2}\\x=-4\end{matrix}\right.\)
\(c,2^x+2^{x+3}=144\\ \Rightarrow2^x+2^x.2^3=144\\ \Rightarrow2^x\left(1+2^3\right)=144\\ \Rightarrow2^x=144:\left(1+2^3\right)\\ \Rightarrow2^x=16\\ \Rightarrow2^x=2^4\\ \Rightarrow x=4\)
\(d,3^{x+2}=9^{x+3}\\ \Rightarrow3^{x+2}=\left(3^2\right)^{x+3}\\ \Rightarrow3^{x+2}=3^{2x+6}\\ \Rightarrow x+2=2x+6\\ \Rightarrow x-2x=6-2\\ \Rightarrow-x=4\\ \Rightarrow x=-4\)
\(e,x^{15}=x^2\\ \Rightarrow x^{15}-x^2=0\\ \Rightarrow x^2\left(x^{13}-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=0\\x^{13}-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
23 tháng 7 2023
a: =>5^x+5^x*25=650
=>5^x*26=650
=>5^x=25
=>x=2
b: =>4x+1=15 hoặc 4x+1=-15
=>4x=-16 hoặc 4x=14
=>x=7/2 hoặc x=-8
c: =>2^x*9=144
=>2^x=16
=>x=4
d: =>2x+2=2x+6
=>2=6(loại)
e: =>x^2(x^13-1)=0
=>x=0 hoặc x=1
PP
1
NH
23 tháng 7 2023
f)
`(2x+1)^3=343`
`(2x+1)^3=7^3`
`=>2x+1=7`
`2x=7-1`
`2x=6`
`x=6:2`
`x=3`
g)
`(x-1)^3 =125`
`(x-1)^3 =5^3`
`=>x-1=5`
`x=6`
h)
`2^(x+2)-2^x=96`
`2^x *2^2 -2^x =96`
`2^x (2^2 -1)=96`
`2^x *3=96`
`2^x =32`
`2^x =2^5`
`=>x=5`
i)
`(x-5)^4 =(x-5)^6` (`x>=5`)
`(x-5)^6 -(x-5)^4 =0`
`(x-5)^4 [(x-5)^2 -1]=0`
`=>x-5=0` hoặc `(x-5)^2 -1=0`
`<=>x=5` hoặc `(x-5)^2 =1`
`<=>x=5` hoặc `x-5=1` hoặc `x-5=-1`
`<=>x=5` hoặc `x=6` hoặc `x=4`
j)
`720:[41-(2x-5)]=2^3 *5`
`720:[41-(2x-5)]=8*5`
`720:[41-(2x-5)]=40`
`41-(2x-5)=720:40`
`41-(2x-5)=18`
`2x-5=41-18`
`2x-5=23`
`2x=28`
`x=14`
PP
3
D
datcoder
CTVVIP
2 tháng 12 2023
y) \(\dfrac{x+2}{4}=\dfrac{3}{6}\)
\(\Leftrightarrow6.\left(x+2\right)=4.3\\ \Leftrightarrow6x+12=12\\ \Leftrightarrow6x=0\\ \Leftrightarrow x=0\)
Vậy x = 0
z) \(\dfrac{2x}{49}=\dfrac{-2}{7}\)
\(\Leftrightarrow2x.7=\left(-2\right).49\\ \Leftrightarrow14x=-98\\ \Leftrightarrow x=-7\)
Vậy x = -7
KV
2 tháng 12 2023
y) (x + 2)/4 = 3/6
x + 2 = 1/2 . 4
x + 2 = 2
x = 2 - 2
x = 0
z) 2x/49 = -2/7
2x = -2/7 . 49
2x = -14
x = -14 : 2
x = -7
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 7 2023
a, 2100 và 10249
10249 = (210)9 = 290
2100 > 290
Vậy 2100 > 290
b, 530 và 6.529
6.529 > 5.529 = 530
vậy 530 < 6.529
c, 298 và 949
(22)49 = 449 < 949
vậy: 298 < 949
d, 1030 và 2100
(103)10 = 100010
2100 = (210)10 = 102410
Vì 100010 < 102410
Nên 1030 < 2100
KV
23 tháng 11 2023
e) Thay x = -3; y = 7; z = -10 vào biểu thức đã cho, ta có:
-3 + 7 + (-10) = -6
f) Thay x = 2; y = -5; z = -8 vào biểu thức, ta có:
-2 - (-5) - (-8) = 13
g) Thay a = -5; b = 9; c = -12 vào biểu thức, ta có:
-5 - 9 - (-12) = -2
PP
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 7 2023
a, \(x^2\) = \(x^3\)
\(x^3\) - \(x^2\) = 0
\(x^2\)( \(x\) -1) = 0
\(\left[{}\begin{matrix}x^2=0\\x-1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(x\) \(\in\) { 0; 1}
e, 32\(x+1\) = 27
\(3^{2x}\)+1 = 33
2\(x\) + 1 = 3
2\(x\) = 2
\(x\) = 1
g, 62 = 6\(x-3\)
2 = \(x-3\)
\(x\) = 3 + 2
\(x\) = 5
H
19 tháng 7 2023
\(a,x^2=x^3\\ \Rightarrow x^2-x^3=0\\ \Rightarrow x^2\left(1-x\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=0\\1-x=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
\(b,3^{2x+1}=27\\ \Rightarrow3^{2x+1}=3^3\\ \Rightarrow2x+1=3\\ \Rightarrow2x=3-1\\ \Rightarrow2x=2\\ \Rightarrow x=2:2\\ \Rightarrow x=1\)
\(c,6^2=6^{x-3}\\ \Rightarrow6^{x-3}=6^2\\ \Rightarrow x-3=2\\ \Rightarrow x=2+3\\ \Rightarrow x=5\)
TT
1
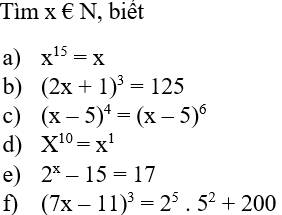
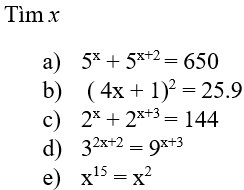
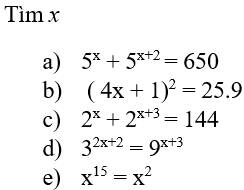
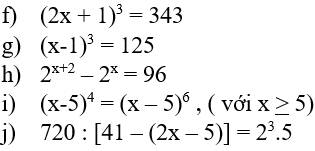
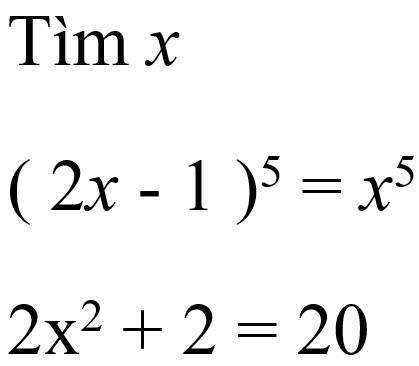
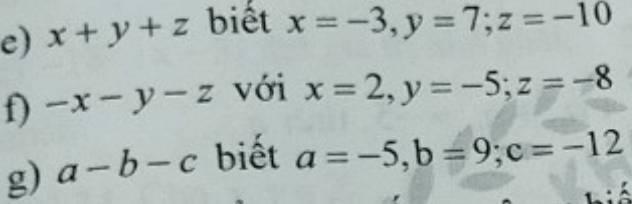
\(a,x^{15}=x\\ \Rightarrow x^{15}-x=0\\ \Rightarrow x\left(x^{14}-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x^{14}-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\left(thoaman\right)\\x=1\left(thoaman\right)\\x=-1\left(loại\right)\end{matrix}\right.\)
\(b,\left(2x+1\right)^3=125\\ \Rightarrow\left(2x+1\right)^3=5^3\\ \Rightarrow2x+1=5\\ \Rightarrow2x=4\\ \Rightarrow x=2\left(thoaman\right)\)
\(c,\left(x-5\right)^4=\left(x-5\right)^6\\ \Rightarrow\left(x-5\right)^4-\left(x-5\right)^6=0\\ \Rightarrow\left(x-5\right)^4\left(1-\left(x-5\right)^2\right)=0\\ \Rightarrow\left[{}\begin{matrix}\left(x-5\right)^4=0\\1-\left(x-5\right)^2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x-5=0\\x-5=1\\x-5=-1\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=5\\x=6\\x=4\end{matrix}\right.\left(thoaman\right)\)
\(d,x^{10}=x^1\\ \Rightarrow x^{10}-x^1=0\\ \Rightarrow x\left(x^9-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x^9-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\left(thoaman\right)\)
\(e,2^x-15=17\\ \Rightarrow2^x=17+15\\ \Rightarrow2^x=32\\ \Rightarrow2^x=2^5\\ \Rightarrow x=5\left(thoaman\right)\)
\(f,\left(7x-11\right)^3=2^5.5^2+200\\ \Rightarrow\left(7x-11\right)^3=32.25+200\\ \Rightarrow\left(7x-11\right)^3=800+200\\ \Rightarrow\left(7x-11\right)^3=1000\\ \Rightarrow\left(7x-11\right)^3=10^3\\ \Rightarrow7x-11=10\\ \Rightarrow7x=21\\ \Rightarrow x=21:7=3\left(thoaman\right)\)
@seven
a: x^15=x
=>x^15-x=0
=>x(x^14-1)=0
=>x=0 hoặc x^14-1=0
=>x=0 hoặc x^14=1
=>x=0;x=1;x=-1
b: =>2x+1=5
=>2x=4
=>x=2
c: =>(x-5)^4[(x-5)^2-1)]=0
=>(x-5)(x-6)(x-4)=0
=>\(x\in\left\{4;5;6\right\}\)
d: x^10=x
=>x^10-x=0
=>x(x^9-1)=0
=>x=0 hoặc x=1
e: 2^x-15=17
=>2^x=32
=>x=5
f: =>(7x-11)^3=1000
=>7x-11=10
=>7x=21
=>x=3