
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số học sinh của 2 lớp lần lượt là : a,b
Ta có: \(\dfrac{a}{8}=\dfrac{b}{7}\) và \(a-b=5\)
Áp dụng tcdtsbn , ta có:
\(\dfrac{a}{8}=\dfrac{b}{7}=\dfrac{a-b}{8-7}=\dfrac{5}{1}=5\)
\(\Rightarrow\left\{{}\begin{matrix}a=40\\b=35\end{matrix}\right.\)

a: Xét ΔADB và ΔADC có
AD chung
DB=DC
AB=AC
Do đó: ΔADB=ΔADC
b: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD là phân giác
c: Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
\(\widehat{EAD}=\widehat{FAD}\)
Do đó: ΔAED=ΔAFD
Suy ra: DE=DF

Câu1:a) \(\left(\dfrac{-2}{3}\right)^2\)+\(\dfrac{-7}{6}\)\(\div\dfrac{3}{8}\)=\(\dfrac{4}{9}\)+\(\dfrac{-7}{6}\times\dfrac{8}{3}\)=\(\dfrac{4}{9}\)+\(\dfrac{-28}{9}\)=\(\dfrac{-24}{9}\)=\(\dfrac{-8}{3}\)
b)=\(\dfrac{-1}{10}\)\(\times\dfrac{9}{2}\)\(-\)\(\dfrac{1}{4}\)=\(\dfrac{-9}{20}-\dfrac{5}{20}\)=\(\dfrac{-14}{20}\)=\(\dfrac{-7}{10}\)
Câu 3:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{7}=\dfrac{x+y+z}{4+5+7}=\dfrac{-32}{16}=-2\)
Do đó: x=-8; y=-10; z=-14

a: Xét ΔABE có
BH là đường cao
BH là đường trung tuyến
Do đó:ΔABE cân tại B
mà BM là đường trung tuyến
nên BM là tia phân giác của góc ABE
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
c: Ta có: ABDC là hình bình hành
nên AB=CD
mà AB=BE
nên CD=BE

a: M(x)+N(x)=7x^3-8x^2-13x-7
b: M(x)+Q(x)=12x^3-2x^2-5x-20
c: N(x)+Q(x)=13x^3-22x-9
d: N(x)-Q(x)=-5x^3-6x^2-8x+13
e: Q(x)-M(x)=6x^3+8x^2-9x-2

Ta có :
\(\left(x+2\right)^2=0\)
\(\Leftrightarrow x+2=0\)
\(\Leftrightarrow x=-2\)





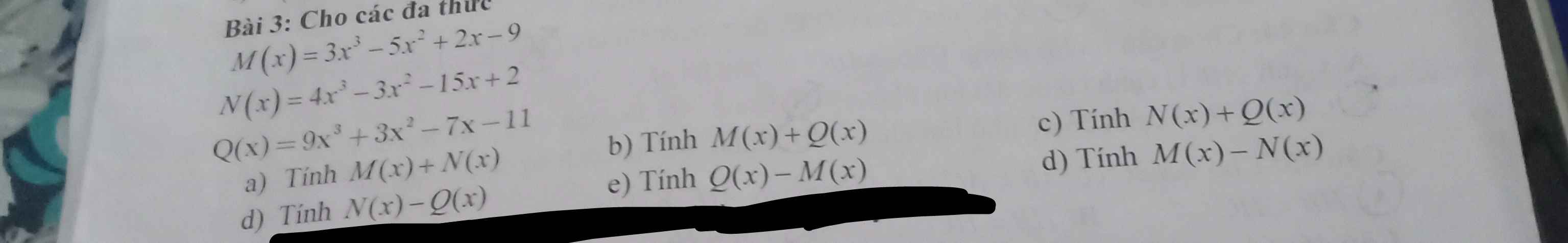
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x^2}{16}=\dfrac{y^2}{9}=\dfrac{x^2+y^2}{16+9}=\dfrac{100}{25}=4\)
Do đó: x=8; y=6