Chỉ mik câu d với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
17 tháng 8 2021
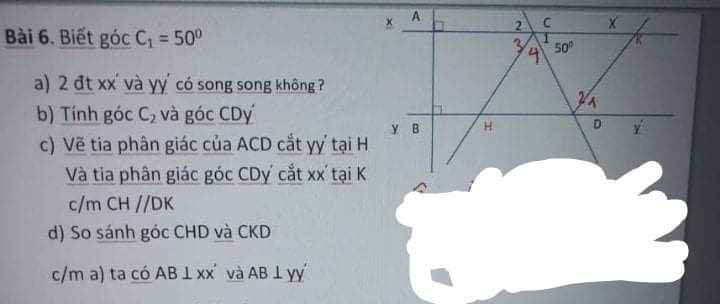
Bài 6:
a:
Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của \(\widehat{HAC}\)
b: Xét ΔAKD vuông tại K và ΔAHD vuông tại H có
AD chung
\(\widehat{KAD}=\widehat{HAD}\)
Do đó: ΔAKD=ΔAHD
Suy ra: AK=AH
ND
Nguyễn Đức Trí
VIP
5 tháng 10 2023
g) \(\left(4^{2x}-1\right)^2=5^2.9\)
\(\Leftrightarrow\left[{}\begin{matrix}4^{2x}-1=5.3\\4^{2x}-1=-5.3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}4^{2x}=16\\4^{2x}=-14\left(loại\right)\end{matrix}\right.\)
\(\Leftrightarrow4^{2x}=4^2\)
\(\Leftrightarrow2x=2\)
\(\Leftrightarrow x=1\)
h) \(2^{x+1}+2^{x+2}+2^{x+3}+...+2^{x+101}=2^{104}-8\)
\(\Leftrightarrow2^{x+1}\left(1+2+2^2+...+2^{100}\right)=2^{104}-8\)
\(\Leftrightarrow2^{x+1}.\left(2^{101}-1\right)=2^{104}-2^3\)
\(\Leftrightarrow2^{x+1}=\dfrac{2^{104}-2^3}{2^{101}-1}\)
\(\Leftrightarrow2^{x+1}=\dfrac{2^3\left(2^{101}-1\right)}{2^{101}-1}\)
\(\)\(\Leftrightarrow2^{x+1}=2^3\)
\(\Leftrightarrow x+1=3\)
\(\Leftrightarrow x=2\)
15 tháng 6 2023
d: BK=BA+AK
BC=BE+EC
mà BA=BE và AK=EC
nên BK=BC
=>góc BKC=góc BCK
3 tháng 10 2021
\(c,\Rightarrow\left|x-\dfrac{1}{9}\right|=-\dfrac{4}{5}\\ \Rightarrow x\in\varnothing\left(\left|x-\dfrac{1}{9}\right|\ge0>-\dfrac{4}{5}\right)\\ d,\Rightarrow\left\{{}\begin{matrix}3x-2=0\\4y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{7}{4}\end{matrix}\right.\\ e,\Rightarrow\left\{{}\begin{matrix}2x+1=0\\x-y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\x=y=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow x=y=-\dfrac{1}{2}\)
20 tháng 12 2021
c: Xét tứ giác ABCK có
M là trung điểm của BK
M là trung điểm của AC
Do đó: ABCK là hình bình hành
Suy ra: AK//BC
20 tháng 12 2021
c: Xét tứ giác ABCK có
M là trung điểm của BK
M là trung điểm của AC
ABCK là hình bình hành
Suy ra: Ak song song BC
kí hiệu AK//BC
15 tháng 7 2021
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
b) Xét ΔABK vuông tại A và ΔIBK vuông tại I có
BK chung
\(\widehat{ABK}=\widehat{IBK}\)(BK là tia phân giác của \(\widehat{ABI}\))
Do đó: ΔABK=ΔIBK(Cạnh huyền-góc nhọn)
Suy ra: KA=KI(hai cạnh tương ứng)
15 tháng 7 2021
c) Ta có: ΔABK=ΔIBK(cmt)
nên BA=BI(Hai cạnh tương ứng)
Xét ΔBAI có BA=BI(cmt)
nên ΔBAI cân tại B(Định nghĩa tam giác cân)
Suy ra: \(\widehat{BAI}=\widehat{BIA}\)(hai góc ở đáy)(1)
Ta có: \(\widehat{BAI}+\widehat{CAI}=\widehat{BAC}\)(tia AI nằm giữa hai tia AB,AC)
nên \(\widehat{BAI}+\widehat{KAI}=90^0\)(2)
Ta có: ΔDAI vuông tại D(gt)
nên \(\widehat{DIA}+\widehat{DAI}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{BIA}+\widehat{DAI}=90^0\)(3)
Từ (1), (2) và (3) suy ra \(\widehat{DAI}=\widehat{KAI}\)
hay AI là tia phân giác của \(\widehat{DAK}\)
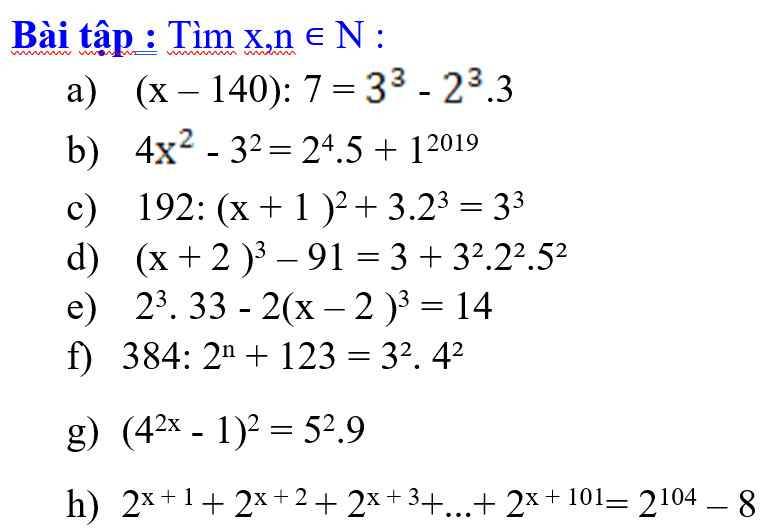
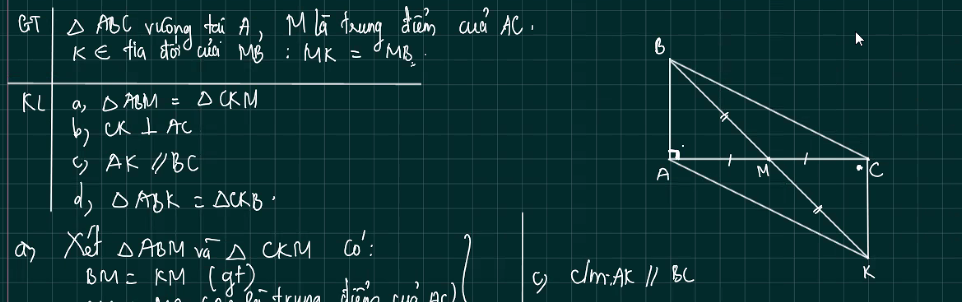
mik chỉ cần câu b thôi
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC
c: Xét ΔABE vuông tại A và ΔCDE vuông tại C có
AB=CD
AE=CE
Do đó: ΔABE=ΔCDE
Suy ra: EB=ED
hay ΔEBD cân tại E