
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{4x^2-4x+9}=3\\ \Rightarrow4x^2-4x+9=9\\ \Rightarrow4x\left(x-1\right)=0\\ \Rightarrow\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Ta có: \(\sqrt{4x^2-4x+9}=3\)
\(\Leftrightarrow4x^2-4x=0\)
\(\Leftrightarrow4x\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)


_không có nghiệm bạn ơi _
<=> 5x2 + 7y2 =-100
Mà 5x2 >= 0 với mọi x thuộc R; 5y2 => 0 với mọi y thuộc R

b: Xét ΔABH vuông tại H có
\(AB^2=AH^2+HB^2\)
hay AH=12(cm)
Xét ΔAHB vuông tại H có
\(\sin\widehat{B}=\cos\widehat{C}=\dfrac{AH}{AB}=\dfrac{12}{13}\)
\(\cos\widehat{B}=\sin\widehat{C}=\dfrac{5}{13}\)
\(\tan\widehat{B}=\cot\widehat{C}=\dfrac{12}{5}\)
\(\cot\widehat{B}=\tan\widehat{C}=\dfrac{5}{12}\)


Ta có: \(\left(\sqrt{5}+1-\sqrt{3}\right)\left(\sqrt{5}-1\right)\)
\(=4-\sqrt{15}+\sqrt{3}\)

\(10,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow x^2+8+x^2+3-2\sqrt{\left(x^2+8\right)\left(x^2+3\right)}=4x^2-4x+1\\ \Leftrightarrow-2\sqrt{x^4+11x^2+24}=2x^2-4x-10\\ \Leftrightarrow-\sqrt{x^4+11x^2+24}=x^2-2x-5\\ \Leftrightarrow x^4+11x^2+24=\left(x^2-2x-5\right)^2\\ \Leftrightarrow x^4+11x^2+24=x^4+4x^2+25-4x^3+20x-10x^2\\ \Leftrightarrow4x^3+17x^2-20x-1=0\\ \Leftrightarrow4x^3-4x^2+21x^2-21x+x-1=0\\ \Leftrightarrow\left(x-1\right)\left(4x^2+21x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\4x^2+21x+1=0\left(1\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-21+5\sqrt{17}}{8}\\x=\dfrac{-21-5\sqrt{17}}{8}\end{matrix}\right.\)
 chỉ mik câu 2 nha
chỉ mik câu 2 nha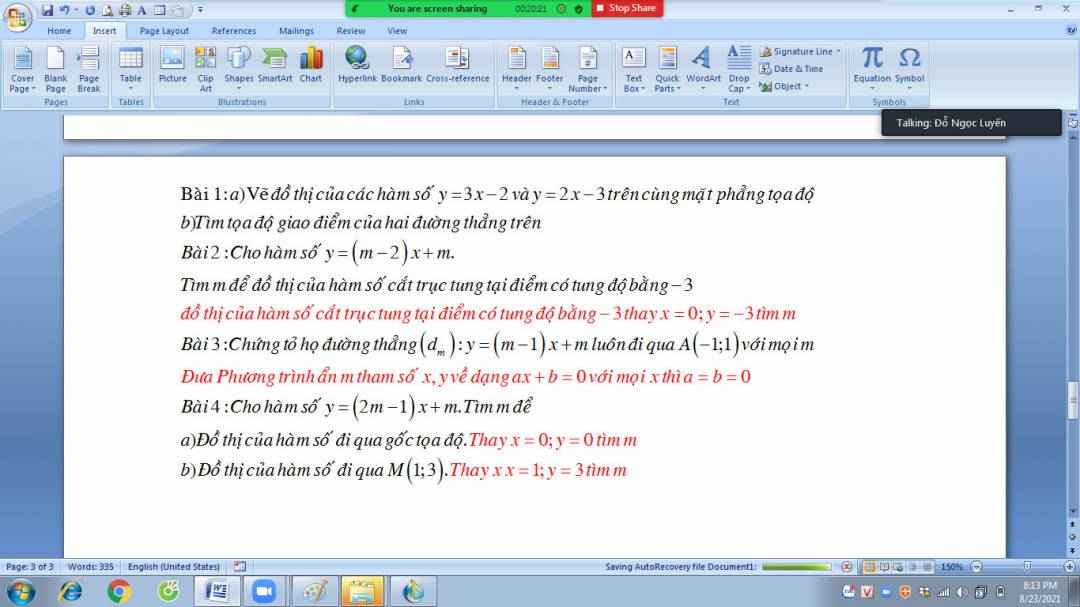


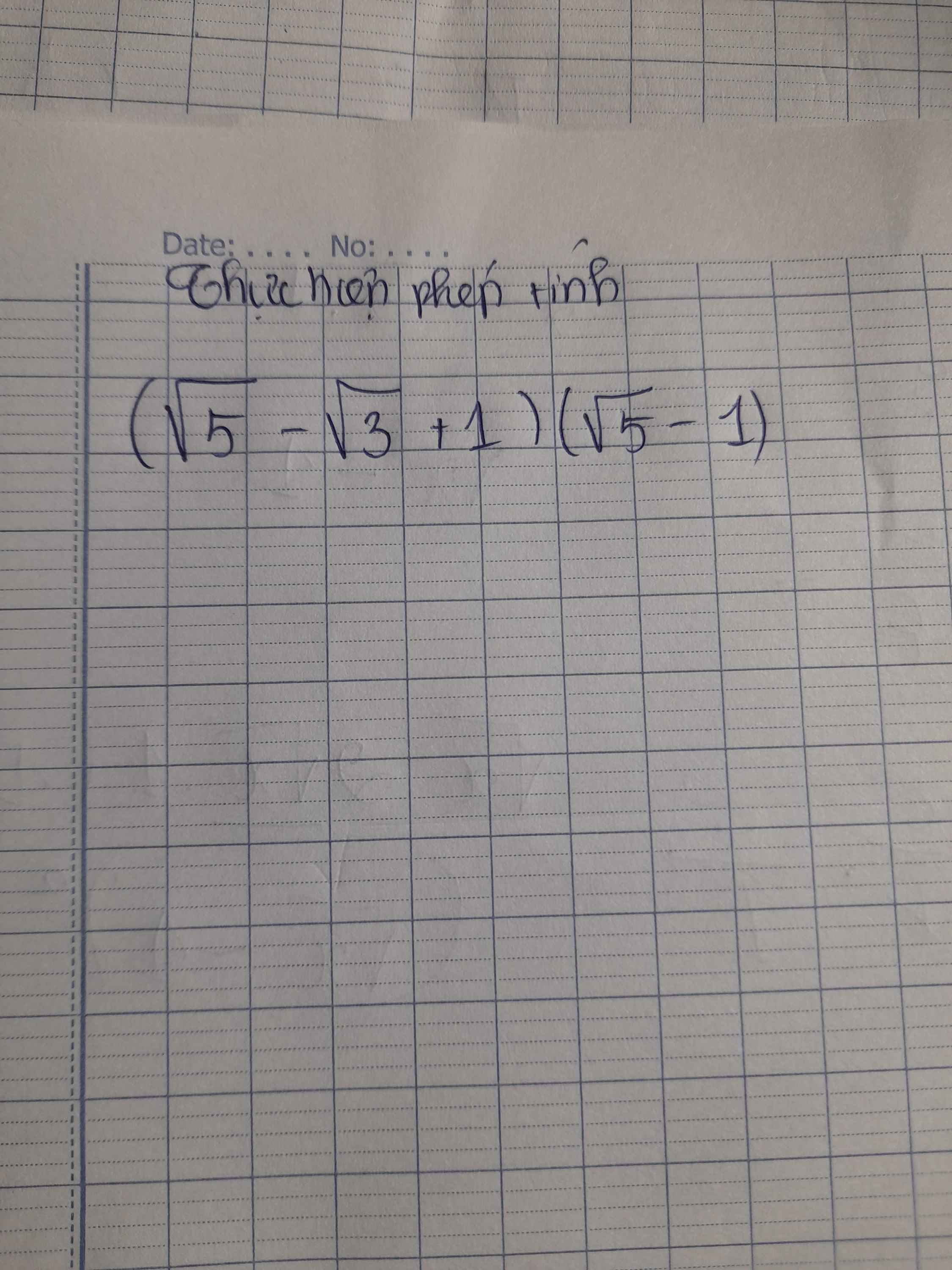
 Giúp mik câu 10 , 12 với nha
Giúp mik câu 10 , 12 với nha