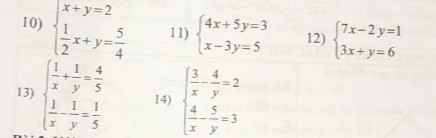Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,P=\dfrac{3\sqrt{x}+6+x+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}-3}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\left(x\ge0;x\ne9;x\ne4\right)\\ P=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{1}{\sqrt{x}+3}=\dfrac{1}{\sqrt{x}-2}\\ b,P< 0\Leftrightarrow\sqrt{x}-2< 0\left(1>0\right)\\ \Leftrightarrow0\le x< 4\)


19
Từ pt đầu ta có:
\(x^2-xy-2xy+2y^2=0\)
\(\Leftrightarrow x\left(x-y\right)-2y\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x-2y\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=y\\x=2y\end{matrix}\right.\)
TH1: \(x=y\) thế xuống pt dưới:
\(y^2-y-y^2=1\Rightarrow y=-1\Rightarrow x=-1\)
TH2: \(x=2y\) thế xuống pt dưới:
\(\left(2y\right)^2-2y-y^2=1\Leftrightarrow3y^2-2y-1=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=2\\y=-\dfrac{1}{3}\Rightarrow x=-\dfrac{2}{3}\end{matrix}\right.\)
Vậy nghiệm của hệ là: \(\left(x;y\right)=\left(-1;-1\right);\left(1;2\right);\left(-\dfrac{1}{3};-\dfrac{2}{3}\right)\)
21.
Từ pt đầu:
\(xy+2=2x+y\Leftrightarrow xy-y+2-2x=0\)
\(\Leftrightarrow y\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(y-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
TH1: \(x=1\) thế xuống pt dưới:
\(2y+y^2+3y=6\Leftrightarrow y^2+5y-6=0\)
\(\Rightarrow\left[{}\begin{matrix}y=1\\y=-6\end{matrix}\right.\)
TH2: \(y=2\) thế xuông pt dưới
\(4x+4+6=6\Rightarrow x=-1\)
Vậy nghiệm của pt là: \(\left(x;y\right)=\left(1;1\right);\left(1;-6\right);\left(-1;2\right)\)

10: =>1/2x=3/4 và x+y=2
=>x=3/4*2=3/2 và y=1/2
11:=>4x+5y=3 và 4x-12y=20
=>17y=-17 và x-3y=5
=>y=-1 và x=3y+5=-3+5=2
12: =>7x-2y=1 và 6x+2y=12
=>13x=13 và 3x+y=6
=>x=1 và y=3
13:=>2/x=1 và 1/x-1/y=1/5
=>x=2 và 1/y=1/2-1/5=3/10
=>y=10/3 và x=2
14: =>12/x-16/y=8 và 12/x-15/y=9
=>-1/y=-1 và 4/x-5/y=3
=>y=1 và 4/x=3+5=8
=>x=1/2 và y=1

Bài 9:
a: a=1; b=-2m; c=-1
Vì a*c<0
nên (1) luôn có 2 nghiệm pb
b: x1^2+x2^2-x1x2=7
=>(x1+x2)^2-3x1x2=7
=>(2m)^2-3*(-1)=7
=>4m^2+3=7
=>m=1 hoặc m=-1


a: Khi m=3 thì (1): x^2-6x+4=0
=>x^2-6x+9-5=0
=>(x-3)^2=5
=>\(x=3\pm\sqrt{5}\)

15. Gọi chiều dài là x, chiều rộng là y (x, y > 0).
- 2 lần chiều dài bằng 3 lần chiều rộng \(\Rightarrow2x=3y\left(1\right)\)
- Nửa chu vi bằng 20 (cm) \(\Rightarrow x+y=20\left(2\right)\)
Từ (1) và (2), ta có hệ phương trình : \(\left\{{}\begin{matrix}2x=3y\\x+y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3y}{2}\\\dfrac{3y}{2}+y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3y}{2}\\3y+2y=40\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3.8}{2}\\y=8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=12\left(tmđk\right)\\y=8\left(tmđk\right)\end{matrix}\right.\)
Vậy : ...