
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 7
A=\(\dfrac{x+2}{\sqrt{x^3}-1}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(x+\sqrt{x}+1\right)}+\dfrac{-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
A=\(\dfrac{x+2+x-1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
A=\(\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)=\(\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+x+1\right)}\)
A=\(\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
bài 8
P=\(\left[\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)^2}\right].\dfrac{\left(x-1\right)^2}{4x}\)
P=\(\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)}.\dfrac{\left(x-1\right)^2}{4x}\)
P=\(\dfrac{2\sqrt{x}}{\left(x-1\right)\left(\sqrt{x}-1\right)}.\dfrac{\left(x-1\right)^2}{4x}\)=\(\dfrac{x-1}{2\sqrt{x}\left(\sqrt{x}-1\right)}\)
P=\(\dfrac{\sqrt{x}+1}{2\sqrt{x}}\)
bài 9
P=\(\left[\dfrac{2\sqrt{xy}}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}-\dfrac{\sqrt{x}+\sqrt{y}}{2\left(\sqrt{x}-\sqrt{y}\right)}\right].\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{4\sqrt{xy}-\left(\sqrt{x}+\sqrt{y}\right)^2}{2\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\dfrac{2\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{2\sqrt{xy}-x-y}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\dfrac{\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{-\left(\sqrt{x}-\sqrt{y}\right)^2}{\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)}.\dfrac{\sqrt{x}}{\sqrt{x}-\sqrt{y}}\)
P=\(\dfrac{-\sqrt{x}}{\sqrt{x}+\sqrt{y}}\)
bài 10
P=\(\left[\dfrac{1}{\sqrt{x}+2}-\dfrac{2}{\left(\sqrt{x}+2\right)^2}\right]:\left[\dfrac{2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{1}{\sqrt{x}-2}\right]\)
P=\(\dfrac{\sqrt{x}+2-2}{\left(\sqrt{x}+2\right)^2}:\dfrac{2-\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
P=\(\dfrac{\sqrt{x}}{\left(\sqrt{x}+2\right)^2}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}{-\sqrt{x}}\)=\(\dfrac{-\left(\sqrt{x}-2\right)}{\sqrt{x}+2}\)

\(1,x=9\Rightarrow A=\dfrac{2\sqrt{9}+1}{\sqrt{9}}=\dfrac{2.3+1}{3}=\dfrac{7}{3}\)
\(2,B=\dfrac{x-3\sqrt{x}+4}{x-2\sqrt{x}}-\dfrac{1}{\sqrt{x}-2}\left(dk:x>0,x\ne4\right)\\ =\dfrac{x-3\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}-\dfrac{1}{\sqrt{x}-2}\\ =\dfrac{x-3\sqrt{x}+4-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{x-4\sqrt{x}+4}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}\left(\sqrt{x}-2\right)}\\ =\dfrac{\sqrt{x}-2}{\sqrt{x}}\)
\(3,P=\dfrac{B}{A}=\dfrac{\sqrt{x}-2}{\sqrt{x}}:\dfrac{2\sqrt{x}+1}{\sqrt{x}}=\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\)
Ta có : \(\left|P\right|+P=0\Leftrightarrow\left|P\right|=-P\)
\(TH_1:x\ge4\\ \dfrac{\sqrt{x}-2}{2\sqrt{x}+1}=-\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\Leftrightarrow\dfrac{2\left(\sqrt{x}-2\right)}{2\sqrt{x}+1}=0\Leftrightarrow2\sqrt{x}=4\Leftrightarrow x=4\left(tm\right)\)
\(TH_2:x< 4\\ -\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}=-\dfrac{\sqrt{x}-2}{2\sqrt{x}+1}\left(LD\right)\)
Vậy \(x=4\) thì thỏa mãn đề bài.

b: Phương trình hoành độ giao điểm của (3) và (1) là:
2x=-x+6
hay x=2
Thay x=2 vào (1), ta được:
y=2x2=4
Phương trình hoành độ giao điểm của (3) và (2) là:
0,5x=-x+6
\(\Leftrightarrow x=4\)
Thay x=4 vào y=-x+6, ta được:
y=-4+6=2

a/
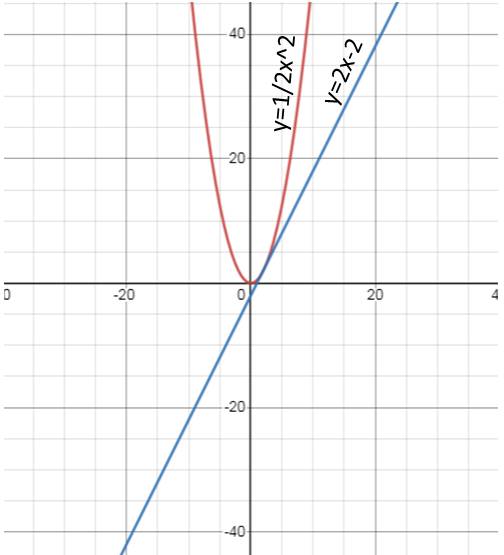
b/
Tọa độ giao điểm của 2 đồ thị là:
\(\dfrac{1}{2}x^2=2x-2\\ \Leftrightarrow\dfrac{1}{2}x^2-2x+2=0\\ \Leftrightarrow x=2\)
b) Phương trình hoành độ giao điểm của (P) và (d):
1/2 x² = 2x - 2
⇔x² = 4x - 4
⇔x² - 4x + 4 = 0
⇔(x - 2)² = 0
⇔x - 2 = 0
⇔x = 2
⇔y = 2.2 - 2 = 2
Vậy tọa độ giao điểm của (P) và (d) là (2;2)

\(\sqrt{9x+9}-2\sqrt{\dfrac{x+1}{4}}=4\left(đk:x\ge-1\right)\)
\(\Leftrightarrow3\sqrt{x+1}-\sqrt{x+1}=4\)
\(\Leftrightarrow2\sqrt{x+1}=4\)
\(\Leftrightarrow\sqrt{x+1}=2\Leftrightarrow x+1=4\Leftrightarrow x=3\left(tm\right)\)

Bài 2:
e) \(\sqrt{4x-8}-12\sqrt{\dfrac{x-2}{9}}=\sqrt{x-2}-12\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{4}.\sqrt{x-2}-12.\sqrt{\dfrac{1}{9}}.\sqrt{x-2}=\sqrt{x-2}-12\)
\(\Leftrightarrow2\sqrt{x-2}-4\sqrt{x-2}=\sqrt{x-2}-12\)
\(\Leftrightarrow3\sqrt{x-2}=12\)
\(\Leftrightarrow\sqrt{x-2}=4\)
\(\Leftrightarrow x-2=16\Leftrightarrow x=18\left(tm\right)\)

1.
Ta có: $4x^2+4x+3=(4x^2+4x+1)+2=(2x+1)^2+2\geq 0+2=2$
$\Rightarrow A=\frac{6}{4x^2+4x+3}\leq \frac{6}{2}=3$
Vậy $A_{\max}=3$. Giá trị này đạt tại $2x+1=0\Leftrightarrow x=\frac{-1}{2}$
2.
$6+4x+x^2=(x^2+4x+4)+2=(x+2)^2+2\geq 0+2=2$
$\Rightarrow \frac{4}{6+4x+x^2}\leq \frac{4}{2}=2$
$\Rightarrow \frac{-4}{6+4x+x^2}\geq -2$
$\Rightarrow B\geq -2$
Vậy $B_{\min}=-2$. Giá trị này đạt tại $x+2=0\Leftrightarrow x=-2$

1) \(=\sqrt{\left(\sqrt{3}-1\right)^2}=\sqrt{3}-1\)
2) \(=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}=\sqrt{3}+\sqrt{2}\)
3) \(=\sqrt{\left(\sqrt{5}-\sqrt{2}\right)^2}=\sqrt{5}-\sqrt{2}\)
5) \(=\sqrt{\left(\sqrt{5}+\sqrt{3}\right)^2}=\sqrt{5}+\sqrt{3}\)
6) \(=\sqrt{\left(\sqrt{7}-\sqrt{3}\right)^2}=\sqrt{7}-\sqrt{3}\)
7) \(=\sqrt{\left(3+\sqrt{2}\right)^2}=3+\sqrt{2}\)


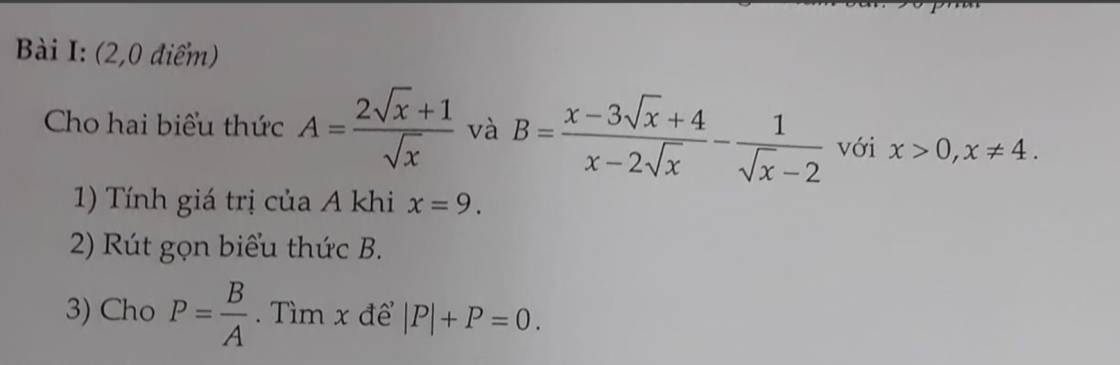
 giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần
giải hộ mk vs chỉ cần có cách làm câu b thôi câu a thì ko cần


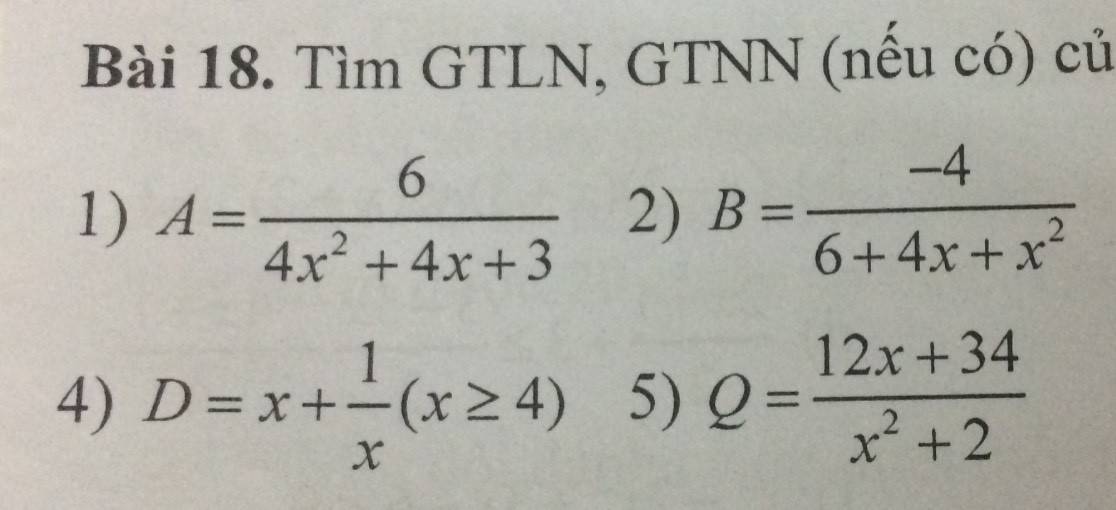
\(P=\dfrac{x-\sqrt{x}+\sqrt{x}-3-\sqrt{x}-3}{x-9}\)
\(=\dfrac{x-\sqrt{x}-6}{x-9}=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+2\right)}{x-9}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\)
4:
a: P>4/5
=>P-4/5>0
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{4}{5}>0\)
=>\(\dfrac{5\sqrt{x}+10-4\sqrt{x}-12}{5\sqrt{x}+15}>0\)
=>\(\sqrt{x}-2>0\)
=>x>4
b: \(P>\dfrac{2\sqrt{x}}{5}\)
=>\(\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{2\sqrt{x}}{5}>0\)
=>\(\dfrac{5\sqrt{x}+10-2x-6\sqrt{x}}{5\sqrt{x}+15}>0\)
=>\(-2x-\sqrt{x}+10>0\)
=>\(-2x-5\sqrt{x}+4\sqrt{x}+10>0\)
=>\(\left(2\sqrt{x}+5\right)\left(-\sqrt{x}+2\right)>0\)
=>\(-\sqrt{x}+2>0\)
=>0<=x<4
5:
a: \(P-\dfrac{1}{2}=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-\dfrac{1}{2}\)
\(=\dfrac{2\sqrt{x}+4-\sqrt{x}-3}{2\sqrt{x}+6}=\dfrac{\sqrt{x}+1}{2\sqrt{x}+6}>0\)
=>P>1/2
b: \(P-1=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}-1=\dfrac{\sqrt{x}+2-\sqrt{x}-3}{\sqrt{x}+3}\)
\(=\dfrac{-1}{\sqrt{x}+3}< 0\)
\(P^2-P=P\left(P-1\right)\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+3}\cdot\dfrac{-1}{\sqrt{x}+3}< 0\)
=>P^2<P
=>P>P^2