Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B.
Gọi H 0 là độ phóng xạ của hạt nhân vừa được tạo ra; H c p là độ phóng xạ cho phép:
Ta có:
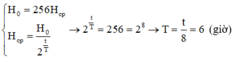
Đáp án B
Gọi H 0 là độ phóng xạ của hạt nhân vừa được tạo ra; H c p là độ phóng xạ cho phép:
Ta có:
H 0 = 256 H c p H c p = H 0 2 t T → 2 t T = 256 = 2 8 → T = t 8 = 6
Đáp án B.
Trong thể tích V 0 = 10 c m 3 = 10 - 2 lít dung dịch với nồng độ 10-3 mol/lít có số mol là n = 10 - 5 mol và có khối lượng là: m 0 = n A = 24 . 10 - 5 g.
Vì N 11 24 a là chất phóng xạ nên sau 6 giờ lượng N 11 24 a còn lại là:
m = m 0 e - λ t = 24 . e ln 2 T t = 18 . 10 - 5 ( g )
Trong thể tích V 0 = 10 c m 3 máu lấy ra có 1 , 875 . 10 - 8 mol của Na, tương ứng với khối lượng chất phóng xạ: m' = n'.A = 1 , 875 . 10 - 8 .24 = 45 . 10 - 8 (g)
Vậy thể tích máu là:
V = m m ' . V 0 = 18 . 10 - 5 45 . 10 - 8 . 10 = 4 . 10 3 c m 3 = 4 ( L í t )
Đáp án: D.
Sau t = T1 = 1h số hạt nhân của chất phóng xạ thứ nhất giảm đi một nửa, còn số hạt nhân của chất phóng xạ thứ hai còn
Như vậy chu kì bán rã của hỗn hợp T > 1h.
Giống bài này bạn nhé Câu hỏi của nguyễn mạnh tuấn - Vật lý lớp 12 | Học trực tuyến
Đáp án B.
Trong thể tích V 0 = 10 c m 3 = 10 - 2 lít dung dịch với nồng độ 10 - 3 mol/lít có số mol là n = 10 - 5 m o l và có khối lượng là: m 0 = n A = 24 . 10 - 5 g .
Vì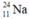 
là chất phóng xạ nên sau 6 giờ lượng 
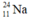còn lại là:
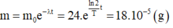
Trong thể tích
V
0
=
10
c
m
3
máu lấy ra có
1
,
875
.
10
-
8
m
o
l
của Na, tương ứng với khối lượng chất phóng xạ:
Vậy thể tích máu là:
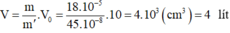
Sau t = T1 = 1h số hạt nhân của chất phóng xạ thứ nhất giảm đi một nửa, còn số hạt nhân của chất phóng xạ thứ hai còn \(\frac{N_{o2}}{2^{\frac{1}{2}}}=\frac{N_{o2}}{\sqrt{2}}>\frac{N_{o2}}{2}\). Như vậy chu kì bán rã của hỗn hợp T > 1h. Vậy chọn A.
Giả sử ban đầu 2 chất đều có số hạt là \(N_0\)
Do vậy, số hạt ban đầu là: \(2.N_0\)
Sau 2h, hỗn hợp 1 còn lại là: \(\dfrac{N_0}{4}\), hỗn hợp 2 còn lại là: \(\dfrac{N_0}{2}\)
Tổng số hạt còn lại của hỗn hợp là: \(N=\dfrac{N_0}{4}+\dfrac{N_0}{2}=\dfrac{3.N_0}{4}\)
Ta có: \(\dfrac{3.N_0}{4}=\dfrac{2N_0}{2^\dfrac{2}{T}}\)
\(\Rightarrow T = \dfrac{2}{\log_2\dfrac{8}{3}}\)
Đáp án D