Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên bờ bên kia của dòng sông lấy điểm B, bờ bên này lấy điểm A đối diện với B. Để đo gián tiếp độ rộng của dòng sông (khoảng cách AB), người ta lấy điểm C bên này sông và cách A một khoảng AC = 80 mét, đặt giác kế tại C và đo được góc ^ACB = 34o. Tính chiều rộng AB của con sông?
( Cho biết: sin34o = 0,56 ; cos34o = 0,83 ; tg34o = 0,67 ; cotg34o = 1,48 )

Xét tam giác ADC có:
\(\widehat{ACB}=\widehat{ADC}+\widehat{DAC}\)(tính chất góc ngoài)
\(\Rightarrow\widehat{DAC}=\widehat{ACB}-\widehat{ACB}=60^0-30^0=30^0\)
\(\Rightarrow\widehat{DAC}=\widehat{ADC}=30^0\)
=> Tam giác ADC cân tại C
=> AC=DC=20m
Áp dụng tslg trong tam giác ABC vuông tại B:
\(AB=sinC.AC=sin60^0.20=10\sqrt{3}\left(m\right)\)
\(BC=cosC.AC=cos60^0.20=10\left(m\right)\)

Câu 3:
Xét ΔBEC vuông tại E và ΔADC vuông tại D có
\(\widehat{BCE}\) chung
Do đó: ΔBEC\(\sim\)ΔADC
Suy ra: \(\dfrac{EC}{DC}=\dfrac{CB}{CA}\)
hay \(CE\cdot CA=CB\cdot CD\left(1\right)\)
Xét ΔBMC vuông tại M có MD là đường cao ứng với cạnh huyền BC
nên \(CD\cdot CB=CM^2\left(2\right)\)
Xét ΔANC vuông tại N có NE là đường cao ứng với cạnh huyền AC
nên \(CN^2=CE\cdot CA\left(3\right)\)
Từ (1), (2) và (3) suy ra CM=CN
hay ΔCMN cân tại C

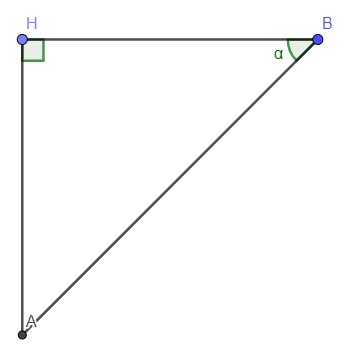
chứng minh: \(1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
xét VT: \(1+tg^2\alpha=1+\dfrac{sin^2\alpha}{cos^2\alpha}\left(vì:tg\left(\alpha\right)=\dfrac{sin\left(\alpha\right)}{cos\left(\alpha\right)}\right)\)
\(=\dfrac{cos^2\alpha+sin^2\alpha}{cos^2\alpha}=\dfrac{1}{cos^2\alpha}\left(vì:sin^2\alpha+cos^2\alpha=1\right)=VP\Rightarrow1+tg^2\alpha=\dfrac{1}{cos^2\alpha}\)
\(\Leftrightarrow1+\dfrac{AH^2}{50^2}=\dfrac{1}{\left(\dfrac{AH^2}{AB^2}\right)}=\dfrac{AB^2}{AH^2}\Leftrightarrow\dfrac{2500+AH^2}{2500}=\dfrac{AB^2}{AH^2}\Leftrightarrow2500AH^2+AH^4=2500AB^2\left(1\right)\)
ta có: \(AH^2+BH^2=AB^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow2500AH^2+AH^4=2500\left(AH^2+50^2\right)\Leftrightarrow AH^4=2500.2500=50^4\Leftrightarrow AH=50\left(m\right)\left(3\right)\)
\(\left(2\right)\left(3\right)\Rightarrow AB=\sqrt{AH^2+BH^2}=\sqrt{50^2+50^2}=50\sqrt{2}\left(m\right)\)
vậy chiều rộng con sông là: \(AH=50\left(m\right)\) và quãng đường đò đã đi là \(AB=50\sqrt{2}\left(m\right)\)

Xét ΔCED có \(\widehat{C}+\widehat{D}+\widehat{E}=180^0\)
=>\(\widehat{D}+105^0+45^0=180^0\)
=>\(\widehat{D}=30^0\)
Xét ΔCED có \(\dfrac{CE}{sinD}=\dfrac{CD}{sinE}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{sin30}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{\dfrac{1}{2}}=40\)
=>\(CD=40\cdot sin45=40\cdot\dfrac{\sqrt{2}}{2}=20\sqrt{2}\)