Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong hình thang ABCD cho ta: SAOD = SBOC = 9 cm2
Xét 2 tam giác AOB và AOD có chúng đường cao kẻ từ A nên 2 đáy OB và OD sẽ tỉ lệ với diện tích.
Suy ra OB/OD = 4/9
Mặt khác, 2 tam giác BOC và DOC có chúng đường cao kẻ từ C nên 2 diện tích sẽ tỉ lệ với 2 đáy.
Mà OB/OD = 4/9 nên SBOC/SDOC = 4/9
Diện tích tam giác DOC: 9 : 4 x 9 = 20,25 (cm2)
Diện tích hình thang ABCD: 4 + 9 + 9 + 20,25 = 42,25 (cm2)

đáp án là 36 cm2 nha
bài này trên violympic vong 16 mình giải rồi
mk biết cách giải nhưng ko biết vẽ hình ,xin lỗi nha

Xét tam giác ABD và BCD có chiều cao bằng nhau đáy AB = 1/2 CD => S_ABD = 1/2 S_BCD
Mặt khác 2 tam giác này có chung đáy BD => chiều cao đỉnh A = 1/2 chiều cao đỉnh C
Xét tam giác ABG và BCG chung đáy BG, chiều cao đỉnh A = 1/2 chiều cao đỉnh C => S_ABG = 1/2 S_BCG
Vậy diện tích tam giac BCG là : 34,5 x 2 = 69 (cm2)
Diện tích ABCD là : (34,5 + 69) + (34,5 + 69) x 2 = 310,5 (cm2)

Lời giải:
Ta có:
$S_{ABD}=S_{ABC}$ (chiều cao bằng nhau và chung đáy $AB$)
$\Rightarrow S_{ADG}=S_{BCG}=129,9$ (cm2)
\(\frac{S_{ADG}}{S_{DCG}}=\frac{AG}{GC}=\frac{S_{ABG}}{S_{BGC}}=\frac{43,3}{129,9}=\frac{1}{3}\Rightarrow S_{DCG}=3\times S_{ADG}=3\times 129,9=389,7\)(cm2)
Diện tích hình thang $ABCD$ là:
$S_{ABG}+S_{BCG}+S_{ADG}+S_{DCG}=43,3+129,9+129,9+389,7=692,8$ (cm2)

Lời giải:
Ta có:
SABD=SABC����=���� (chiều cao bằng nhau và chung đáy AB��)
⇒SADG=SBCG=127,6⇒����=����=129,9 (cm2SADGSDCG=AGGC=SABGSBGC=31,9127,6=14⇒SDCG=4×SADG=4×127,6=510,4(cm2)��������=����=��������=43,3129,9=13⇒����=3×����=3×129,9=389,7(cm2)
Diện tích hình thang ABCD���� là:
SABG+SBCG+SADG+SDCG=31,9+127,6+127,6+510,4=797,5 (cm2)����+����+����+����=43,3+129,9+129,9+389,7=692,8 (cm2)

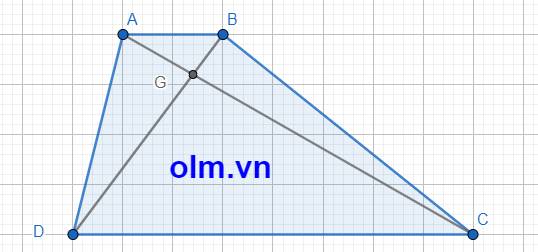
SABD = SABC (vì hai tam giác có chiều cao bằng nhau và chung cạnh đáy AB)
⇒ SABG + SADG = SABG + SBCG ⇒ SADG = SBGC = 170,8 cm2
\(\Delta\)ABG và \(\Delta\)BGC có chung chiều cao hạ từ đỉnh B xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và bằng:
\(\dfrac{AG}{GC}\) = \(\dfrac{42,7}{170,8}\) = \(\dfrac{1}{4}\)
\(\Delta\)AGD và \(\Delta\)DGC có chung chiều cao hạ từ đỉnh D xuống đáy AC nên tỉ số diện tích hai tam giác là tỉ số hai cạnh đáy và băng
\(\dfrac{AG}{GC}\) = \(\dfrac{1}{4}\)
⇒SDGC = SAGD : \(\dfrac{1}{4}\)
Diện tích tam giác DGC là: 170,8 : \(\dfrac{1}{4}\) = 683,2 (cm2)
Diện tích hình thang ABCD là:
42,7 + 170,8 + 170,8 + 683,2 = 1067,5 (cm2)
Đáp số: 1067,5 cm2
\(\dfrac{S_{AOB}}{S_{BOC}}=\dfrac{12}{36}=\dfrac{1}{3}\)
=>\(\dfrac{OA}{OC}=\dfrac{1}{3}\)
Vì AB//CD nên \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{1}{3}\)
Vì OB/OD=1/3 nên \(S_{AOB}=\dfrac{1}{3}\cdot S_{AOD}\)
=>\(S_{AOD}=3\cdot S_{AOB}=36\left(cm^2\right)\)
Vì AO/OC=1/3 nên \(S_{AOD}=\dfrac{1}{3}\cdot S_{DOC}\)
=>\(S_{DOC}=3\cdot36=108\left(cm^2\right)\)
\(S_{ABCD}=S_{AOB}+S_{BOC}+S_{DOC}+S_{AOD}\)
\(=12+36+36+108=120+72=192\left(cm^2\right)\)