K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 3 2022
7.
\(u_1=\dfrac{1+1}{2.1+1}=\dfrac{2}{3}\) ; \(u_2=\dfrac{2+1}{2.2+1}=\dfrac{3}{5}\Rightarrow u_1-u_2=\dfrac{2}{3}-\dfrac{3}{5}=\dfrac{1}{15}>0\)
\(\Rightarrow\) Dãy đã cho là dãy giảm nên đáp án B sai
8.
Đề bài sai, rõ ràng \(u_1+u_2>1\) nhưng tất cả công thức trong dãy đều cho tổng nhỏ hơn 1
9.
\(u_{n+1}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}\); \(v_1=u_1=\dfrac{1}{2}\)
\(v_{n+1}=v_n+\dfrac{1}{\left(n+1\right)\left(n+2\right)}=v_n+\dfrac{1}{n+1}-\dfrac{1}{n+2}\)
\(\Rightarrow v_{n+1}+\dfrac{1}{\left(n+1\right)+1}=v_n+\dfrac{1}{n+1}\)
Đặt \(v_n+\dfrac{1}{n+1}=x_n\Rightarrow\left\{{}\begin{matrix}x_1=v_1+\dfrac{1}{2}=1\\x_{n+1}=x_n=...=x_1=1\end{matrix}\right.\)
\(\Rightarrow v_n+\dfrac{1}{n+1}=1\Rightarrow v_n=1-\dfrac{1}{n+1}=\dfrac{n}{n+1}\)
MT
2
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
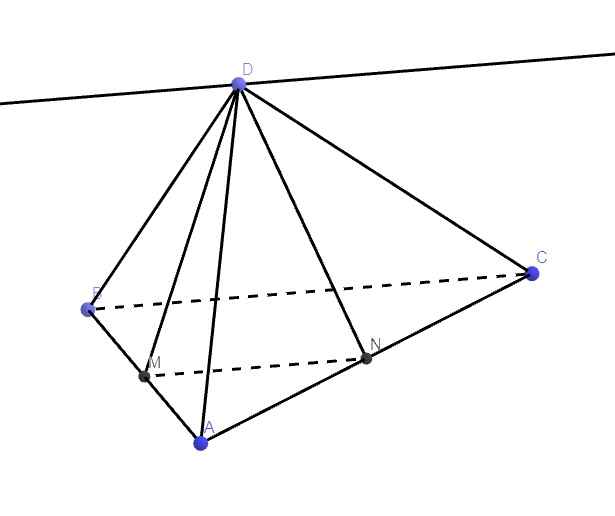
Giả thiết suy ra MN là đường trung bình tam giác ABC \(\Rightarrow MN||BC\)
Mà \(\left\{{}\begin{matrix}MN=\left(DMN\right)\cap\left(ABC\right)\\BC=\left(BCD\right)\cap\left(ABC\right)\end{matrix}\right.\)
Và D là 1 điểm chung của (BCD) và (DMN)
\(\Rightarrow\) Giao tuyến của (BCD) và (DMN) phải là 1 đường thẳng qua D và song song MN (hoặc BC)
AW
2
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
17.
Gọi số vi khuẩn ban đầu là x
Sau 5 phút số vi khuẩn là: \(x.2^5=64000\Rightarrow x=2000\)
Sau k phút:
\(2000.2^k=2048000\Rightarrow2^k=1024=2^{10}\)
\(\Rightarrow k=10\)
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 3 2022
18.
\(S_{2019}=\left(\dfrac{1}{2}\right)^1+1+\left(\dfrac{1}{2}\right)^2+1+...+\left(\dfrac{1}{2}\right)^{2019}+1\)
\(=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}+2019\)
Xét \(S=\left(\dfrac{1}{2}\right)^1+\left(\dfrac{1}{2}\right)^2+...+\left(\dfrac{1}{2}\right)^{2019}\) là tổng cấp số nhân với \(\left\{{}\begin{matrix}u_1=\dfrac{1}{2}\\q=\dfrac{1}{2}\\n=2019\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{1}{2}.\dfrac{\left(\dfrac{1}{2}\right)^{2019}-1}{\dfrac{1}{2}-1}=1-\dfrac{1}{2^{2019}}\)
\(\Rightarrow S_{2020}=2019+S=2020-\dfrac{1}{2^{2019}}\)
19. C là khẳng định sai, ví dụ: \(u_n=2\) ; \(v_n=-\dfrac{1}{n}\)
SM
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
71.
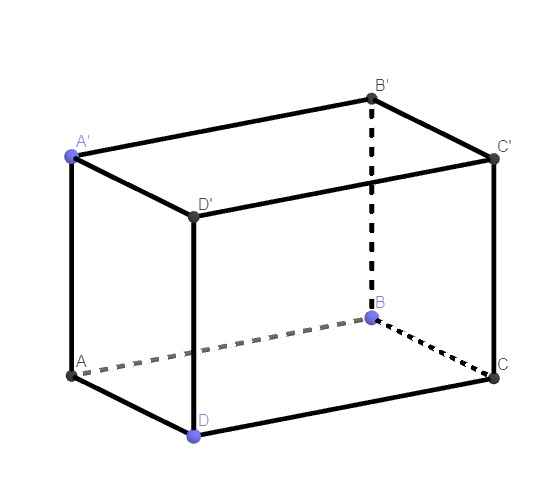
\(\left\{{}\begin{matrix}BB'\perp\left(ABCD\right)\\BB'\in\left(ABB'A'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(ABB'A'\right)\)
74.
\(\left\{{}\begin{matrix}DD'\perp\left(ABCD\right)\\DD'\in\left(CDD'C'\right)\end{matrix}\right.\) \(\Rightarrow\left(ABCD\right)\perp\left(CDD'C'\right)\)
MT
2
26 tháng 8 2021
Khoảng cách từ M để ABC bằng MA
Khoảng cách từ EF đến SAB bằng EM = AF
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 8 2021
Do MN là đường trung bình tam giác ABC \(\Rightarrow MN||AB\) mà \(AB||CD\Rightarrow MN||CD\)
MN và (ABCD) không có điểm chung \(\Rightarrow MN||\left(ABCD\right)\)
MN và (SCD) không có điểm chung \(\Rightarrow MN||\left(SCD\right)\)
MN nằm trên (SAB) nên MN không song song (SAB)
Vậy MN song song với cả (ABCD) và (SCD)
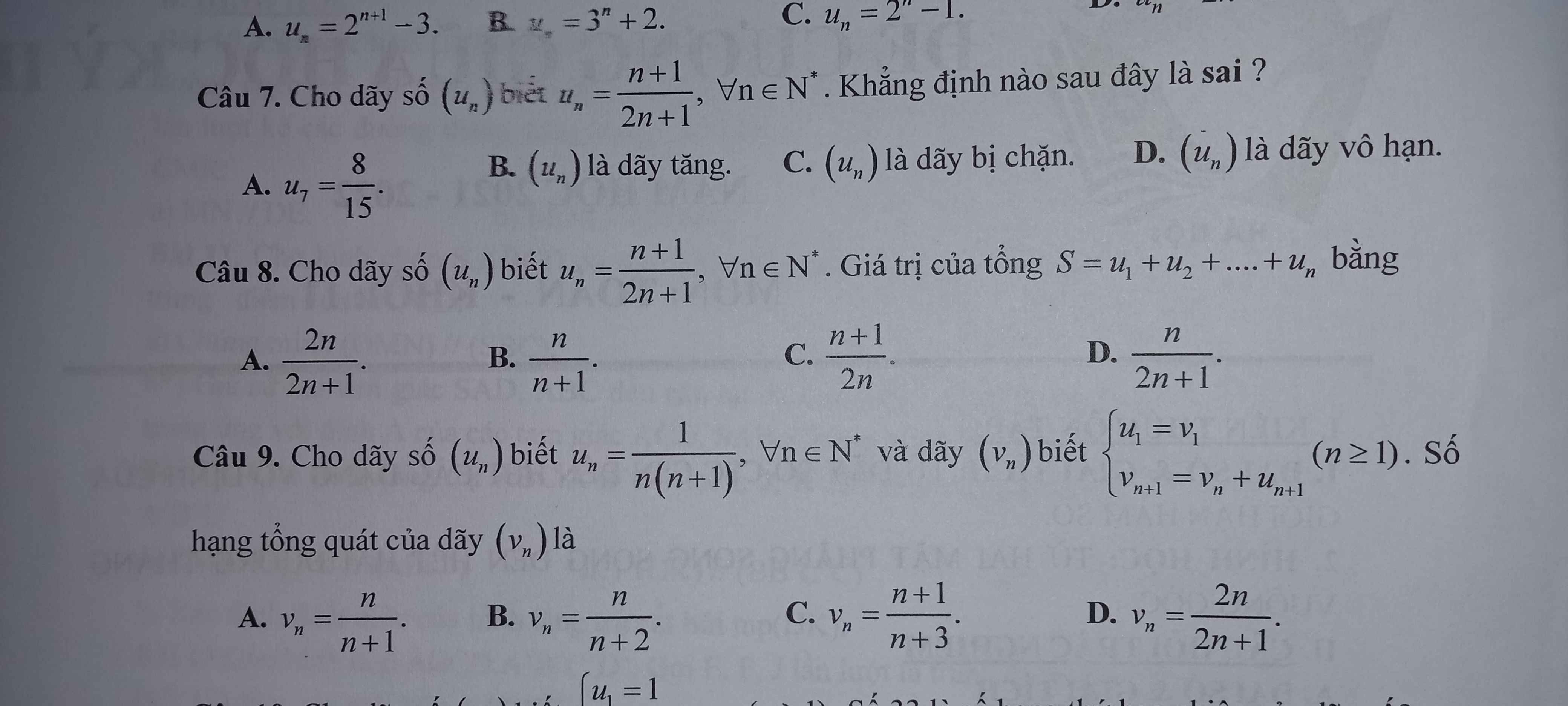
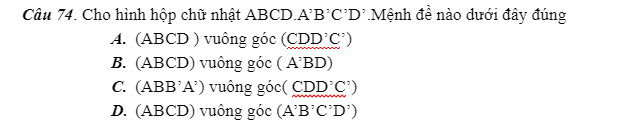
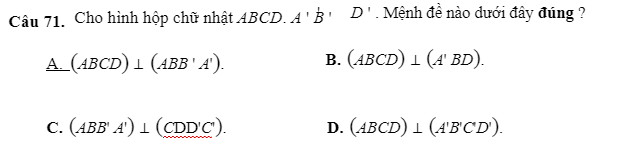
27.
Gọi 3 cạnh của tam giác lần lượt là a;b;c với c là cạnh huyền
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=3\\a+c=2b\\a^2+b^2=c^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b+c=3\\3-b=2b\\a^2+b^2=c^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=2-c\\b=1\\\left(2-c\right)^2+1=c^2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{3}{4}\\b=1\\c=\dfrac{5}{4}\end{matrix}\right.\)
28.
Cấp số cộng thứ nhất có \(u_1=4;d=3\Rightarrow u_n=4+3\left(n-1\right)=3n+1\)
Cấp số cộng thứ hai có \(u_1=1;d=5\Rightarrow u_m=1+5\left(m-1\right)=5m-4\)
Trong đó \(1\le m;n\le100\) (do mỗi CSC có 100 số hạng)
Số có mặt trong cả 2 CSC thỏa mãn:
\(3n+1=5m-4\)
\(\Leftrightarrow3n=5\left(m-1\right)\)
\(\Rightarrow n⋮5\Rightarrow n=5k\)
\(\Rightarrow1\le5k\le100\Rightarrow1\le k\le20\)
\(\Rightarrow\) Có 20 giá trị k hay có 20 số thỏa mãn