Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Câu 20: Cho hình vẽ biết m//n và góc xHm= 2x + 170 và góc xHD = x + 130 Tính góc nKy?
A. 1800 B.1170 C.730 D.630
1:
góc AOC=góc BOD
góc AOC+góc BOD=130 độ
=>góc AOC=góc BOD=130/2=65 độ
góc AOD=góc BOC=180-65=115 độ
2:
a: góc x'Oy'=góc xOy=60 độ
góc xOy'=góc x'Oy=180-60=120 độ
b: góc xOm=60/2=30 độ
góc x'On=60/2=30 độ
=>góc xOm=góc x'On
=>góc xOm+góc xOn=180 độ
=>Om và On là hai tia đối nhau
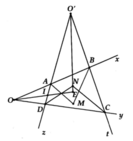
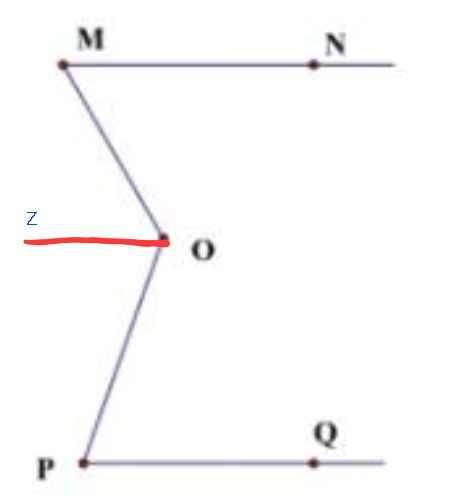Vẽ tia Oz //MN
⇒ ∠MOz = ∠OMN = 60⁰
⇒ ∠zOP = ∠MOP - ∠MOz
= 130⁰ - 60⁰
= 70⁰
Để MN // PQ thì MN // Oz
⇒ ∠P = ∠OPQ = ∠POz = 70⁰ (so le trong)
Ω
ta có góc A+ góc D = 180 độ
=> góc D = 180 - góc A = 180-60 = 120 độ
góc B + góc C = 180 độ
=> góc B = 180 - góc C = 180-130=50 độ
Gọi số đã cho là : ab
( a,b thuộc N , a # 0, a,b < 10)
Số mới có dạng : ba
Theo bài ra ta có:
ab . ba = 3154
Gọi số nhỏ là ab. Ta có :
ab - ( a + b ) = 27
a 10 + b -a - b = 27
9a = 27
a = 27 : 9
a = 3
Từ đó ta có : 3b . b3 = 3154
Vì 3.b có tận cùng là 4 nên b bằn 8. Vậy số cần tìm là 38
\(\left\{{}\begin{matrix}a//b\\a\perp AB\end{matrix}\right.\Rightarrow b\perp AB\Rightarrow\widehat{B_1}=90^0\\ a//b\Rightarrow\widehat{D_1}+\widehat{C}=180^0\left(2.góc.trong.cùng.phía\right)\\ \Rightarrow\widehat{D_1}=180^0-130^0=50^0\)
Ta có: a//b
Mà \(a\perp AB\)
=> \(b\perp AB\Rightarrow\widehat{B_1}=90^0\)
Ta có: a//b
\(\Rightarrow\widehat{D_1}+\widehat{DCB}=180^0\)(trong cùng phía)
\(\Rightarrow\widehat{D_1}=180^0-\widehat{DCB}=180^0-130^0=50^0\)
Vì ^xHm kề bù với ^xHD
⇒ ^xHm+^xHD\(=180^o\)
⇒ \(2x+17^o+x+13^o=180^o\)
⇒ \(3x+30^o=180^o\)
⇒ \(3x=150^o\)
⇒ \(x=50^o\)
⇒ ^xHm\(=\)\(2.50+17\)
\(=117^o\)
mà ^xHm=^nKy đồng vị
⇒ ^nky\(=117^o\)