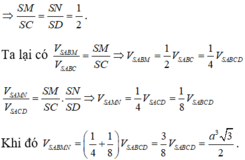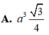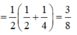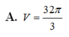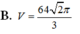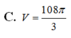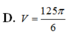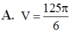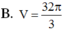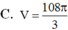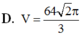Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
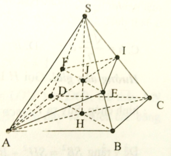
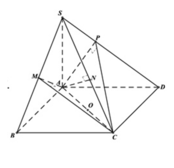
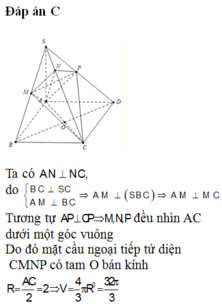
Do các cạnh bên bằng nhau nên hình chiếu của S lên (ABCD) phải trùng với tâm H của hình vuông ABCD.
Dễ thấy I là trung điểm của SC, vì BD ⊥ SC, nên BD//(P). Do đó EF // BD. Để ý rằng EF đi qua trọng tâm J của tam giác SDB.
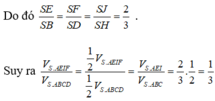

Đáp án B
Hướng dẫn giải:
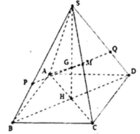
Gọi H là tâm của đáy khi đó S H ⊥ ( A B C D )
Lại có S H = H A tan 60 o = a 6 2
V S . A B C D = 1 3 S H . S A B C D = a 3 6 6
Mặt khác, gọi G = S H ∩ A M
⇒ G là trọng tâm của tam giác SAC.
Do đó S G S H = 2 3
Qua G dựng đường thẳng song song với BD cắt SB, SD lần lượt tại P và Q
Khi đó V S . A B M V S . A B C = S P S B . S M S C = 1 3
từ đó suy ra V S . A P M Q V S . A B C D = 1 3
Do vậy V S . A P M Q = a 3 6 18
⇒ 18 V a 3 = 6

Chọn A
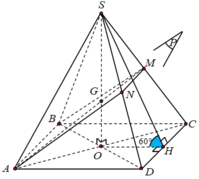
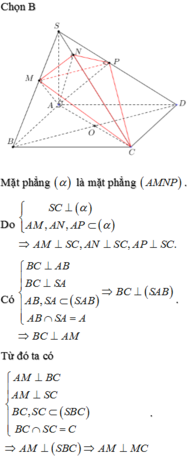
Gọi H là trung điểm cạnh CD và O là tâm hình vuông ABCD.
Ta có S. ABCD là hình chóp tứ giác đều nên các mặt bên hợp với đáy các góc bằng nhau
Giả sử S C D , A B C D ^ = S H O ^ = 60 o
Tam giác SHO vuông tại O có:
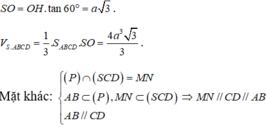
Mà G là trọng tâm tam giác SAC nên G cũng là trọng tâm tam giác SBD