K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
16 tháng 6 2019
Phương pháp:
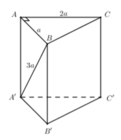
Sử dụng công thức tính thể tích lăng trụ V = S đ á y . h
Cách giải:
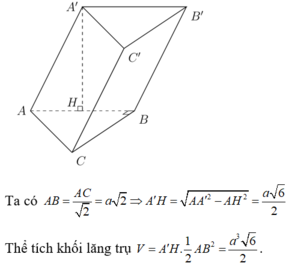
Trong tam giác vuông A'AB có:
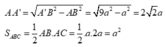
Vậy ![]()
Chọn: C

CM
19 tháng 2 2019
Chọn C.
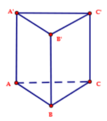
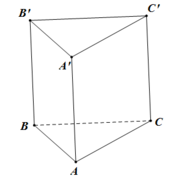
Tam giác ABC là tam giác vuông cân tại B và AC = 2a ![]()
Diện tích của tam giác ABC: ![]()
Thể tích của khối lăng trụ ABC.A'B'C': ![]()
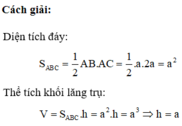
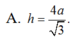
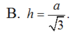
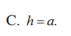
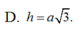
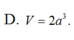
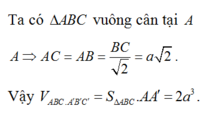
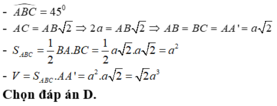

đây là toán lớp 12 à ./ sao dễ thế bây h tui mới biết kiến thức của mình lớp 12 cớ đấy ( nói zui thui)
câu 2
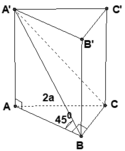
từ A hạ đường trung tuyến \(AM\perp BC\)( tam giác ABC zuông cân tại A)
từ B hạ\(BM\perp BC\)( tam giác B'BC cân tại B (gt)
=> M là hình chiếu của B' ( ABC)
=> B'M là đường cao
xét tam giác zuông MB'A zuông tại M
=>\(B'M^2+MA^2=AB'^2\Rightarrow B'M=\sqrt{AB'^2-MA^2}\)
ta lại có
\(\frac{1}{MA^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=>\frac{1}{MA^2}=\frac{1}{a^2}+\frac{1}{a^2}=>MA=\frac{a}{\sqrt{2}}\)
=> \(B'M=\sqrt{\left(2a\right)^2-\left(\frac{a}{\sqrt{2}}\right)^2}=\frac{a\sqrt{14}}{2}\)
câu 1: cho tứ diện lồi ABCD biết ∠ABC= ∠ADC=90 độ, ∠BAD=150 độ và BD=2a. tính AC
tam giác ABD nội tiếp đường kính AC
áp dụng định lý sin trong tam giác ABD là đc nha