Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo em, tia Oz đã chia\(\widehat {xOy}\) thành hai góc bằng nhau

a) Đỉnh của góc xOz và zOy cùng là đỉnh O
2 góc xOz và zOy có chung cạnh Oz, cạnh còn lại (Ox và Oy) là 2 tia đối nhau.
b) \(\widehat{xOz}=40^0, \widehat{zOy}=140^0\)
Ta được: \(\widehat{xOz}+\widehat{zOy}=40^0+140^0=180^0\)

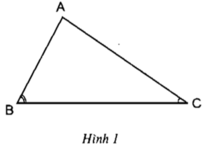
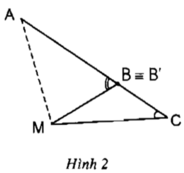
Ta có: góc AB’M là góc ngoài của tam giác MB’C
Nên ∠(BMC) + ∠C= (AB'M) ⇒ ∠(AB'M) > ∠C

a) Ta có : \(\widehat{xOy}+\widehat{O_2}=150^o\left(gt\right)\)
và \(\widehat{xOy}-\widehat{O_2}=90^o\)
\(\Rightarrow\widehat{xOy}=\left(150^o+90^o\right)\div2=120^o\)
\(\Rightarrow\widehat{O_2}=150^o-120^o=30^o\)
b) Ta có : \(\widehat{O_1}+\widehat{O_2}=\widehat{xOy}\)
\(\widehat{O_1}=\widehat{xOy}-\widehat{O_2}\)
\(\widehat{O_1}=90^o\)
Ta có : \(\widehat{O_2}+\widehat{O_3}=180^o\)( kề bù )
\(30^o+\widehat{O_3}=180^o\)
\(\widehat{O_3}=180^o-30^o\)
\(\widehat{O_3}=150^o\)
mà \(\widehat{O_1}=90^o\left(cmt\right)\)
\(\Rightarrow\widehat{O_1}< \widehat{O_3}\)

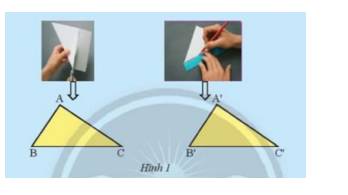
Ta thấy 2 tam giác có các cặp góc bằng nhau \(\widehat A = \widehat {A'}\); \(\widehat B = \widehat {B'}\); \(\widehat C = \widehat {C'}\)
2 tam giác có các cặp cạnh bằng nhau AC = A’C’; AB = A’B’; BC = B’C’

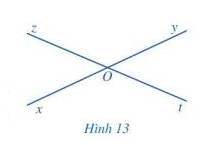
a) Cạnh Ox của góc xOz là tia đối của cạnh Oy của góc yOt.
b) Cạnh Oz của góc xOz là tia đối của cạnh Ot của góc yOt.

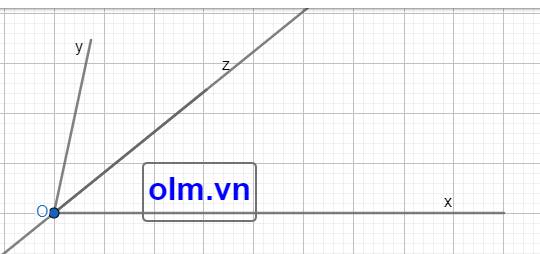
a, Trên cùng một nửa mặt phẳng có bờ là tia ox vì \(\widehat{xOy}\) > \(\widehat{xOz}\) nên Oz nằm giữa hai tia Oy và Ox.
b, \(\widehat{xOy}\) = \(\widehat{xOz}\) + \(\widehat{zOy}\) ⇒ \(\widehat{zOy}\) = 800 - 400 = 400
c, Oz nằm giữa hai tia Oy và Ox và \(\widehat{zOy}\) = \(\widehat{xOz}\) nên OZ là tia phân giác của góc xOy
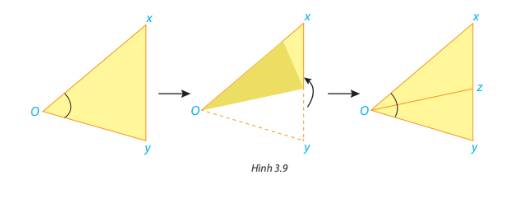
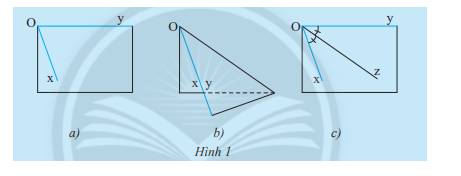
a) Tia Oz nằm giữa hai cạnh của góc xOy.
b) \(\widehat {xOz} = \widehat {zOy}\)