
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


[cos (3x + π/2) + 1] . sin (x + π/5) = 0 (*)
<=> cos (3x + π/2) + 1 = 0 hoặc sin (x + π/5) = 0
<=> cos (3x + π/2) = -1 hoặc sin (x + π/5) = 0
<=> 3x + π/2 = π + k2 π hoặc x + π/5 = k π (k∈Z)
<=> x = π/6 + k2 π/3 hoặc x = - π/5 + k π (k∈Z)
Vậy phương trình (*) có các họ nghiệm …

Ớ :D? Này hình như là đề thi chọn HSG Quốc gia môn Toán đúng ko nhờ :D? Thằng bạn kêu tui làm thử mà nhìn đề xong tui shock nặng luôn :b Lót dép hóng ai đó làm :3
Ò đúng rồi, đề thi HSG đó, con bạn mình nó kêu đi hỏi hộ nó để nó so keys, cơ mà thôi chắc không cần nữa rồi :v

Câu d có thể liệt kê ra, hoặc làm như sau:
Dễ dàng nhận ra với lần đầu tiên tung ra mặt có số chấm là 1,2,5,6 thì chỉ có 1 khả năng để 2 lần cách nhau 2 chấm là 3,4,3,4
Còn với các chấm 3 và 4 xuất hiện ở lần đầu thì có 2 khả năng tung lần 2 để 2 lần gieo cách nhau 2 chấm
Như vậy n(C) = 4.1 + 2.2 = 8

\(\lim\limits_{x\rightarrow1}\frac{x^{n+1}-\left(n+1\right)x+n}{\left(x-1\right)^2}=\lim\limits_{x\rightarrow1}\frac{\left(n+1\right)x^n-\left(n+1\right)}{2\left(x-1\right)}=\lim\limits_{x\rightarrow1}\frac{n\left(n+1\right)x^{n-1}}{2}=\frac{n\left(n+1\right)}{2}\)
Phức tạp hơn thì làm như sau:
\(\lim\limits_{x\rightarrow1}\frac{x\left(x^n-nx+n-1\right)+n\left(x^2-2x+1\right)}{\left(x-1\right)^2}\)
\(=\lim\limits_{x\rightarrow1}\frac{x\left(x-1\right)^2\left(x^{n-1}+2x^{n-2}+...+\left(n-2\right)x+n-1\right)+n\left(x-1\right)^2}{\left(x-1\right)^2}\)
\(=\lim\limits_{x\rightarrow1}\left[x\left(x^{n-1}+2x^{n-2}+...+n-1\right)+n\right]\)
\(=\left(1+2+...+n-1+n\right)=\frac{n\left(n+1\right)}{2}\)


5.
\(\lim\dfrac{n+1}{n^2-2}=\lim\dfrac{n^2\left(\dfrac{1}{n}+\dfrac{1}{n^2}\right)}{n^2\left(1-\dfrac{2}{n^2}\right)}=\lim\dfrac{\dfrac{1}{n}+\dfrac{1}{n^2}}{1-\dfrac{2}{n^2}}=\dfrac{0+0}{1-0}=0\)
\(\lim\dfrac{n\left(n+1\right)}{\left(n+4\right)^3}=\lim\dfrac{n^3\left(\dfrac{1}{n}+\dfrac{1}{n^2}\right)}{n^3\left(1+\dfrac{4}{n}\right)^3}=\lim\dfrac{\dfrac{1}{n}+\dfrac{1}{n^2}}{\left(1+\dfrac{4}{n}\right)^3}=\dfrac{0+0}{\left(1+0\right)^3}=0\)
\(\lim\dfrac{3n^3-2n+5}{2n^2+5n-3}=\lim\dfrac{n^3\left(3-\dfrac{2}{n^2}+\dfrac{5}{n^3}\right)}{n^3\left(\dfrac{2}{n}+\dfrac{5}{n^2}-\dfrac{3}{n^3}\right)}=\lim\dfrac{3-\dfrac{2}{n^2}+\dfrac{5}{n^3}}{\dfrac{2}{n}+\dfrac{5}{n^2}-\dfrac{3}{n^3}}=\dfrac{3}{0}=+\infty\)
\(\lim\dfrac{2n^3}{n^4+3n^2+1}=\lim\dfrac{n^4\left(\dfrac{2}{n}\right)}{n^4\left(1+\dfrac{3}{n^2}+\dfrac{1}{n^4}\right)}=\lim\dfrac{\dfrac{2}{n}}{1+\dfrac{3}{n^2}+\dfrac{1}{n^4}}=\dfrac{0}{1}=0\)
6.
\(\lim\dfrac{3^n-4^n+5^n}{3^n+4^n-5^n}=\lim\dfrac{5^n\left[\left(\dfrac{3}{5}\right)^n-\left(\dfrac{4}{5}\right)^n+1\right]}{5^n\left[\left(\dfrac{3}{5}\right)^n+\left(\dfrac{4}{5}\right)^n-1\right]}=\lim\dfrac{\left(\dfrac{3}{5}\right)^n-\left(\dfrac{4}{5}\right)^n+1}{\left(\dfrac{3}{5}\right)^n+\left(\dfrac{4}{5}\right)^n-1}=\dfrac{0+0+1}{0+0-1}=-1\)
\(\lim\dfrac{1+3^n}{4+3^n}=\lim\dfrac{3^n\left[\left(\dfrac{1}{3}\right)^n+1\right]}{3^n\left[4.\left(\dfrac{1}{3}\right)^n+1\right]}=\lim\dfrac{\left(\dfrac{1}{3}\right)^n+1}{4.\left(\dfrac{1}{3}\right)^n+1}=\dfrac{0+1}{4.0+1}=1\)
\(\lim\dfrac{4.3^n+7^{n+1}}{2.5^n+7^n}=\lim\dfrac{7^n\left[4.\left(\dfrac{3}{7}\right)^n+7\right]}{7^n\left[\left(\dfrac{5}{7}\right)^n+1\right]}=\lim\dfrac{4.\left(\dfrac{3}{7}\right)^n+7}{\left(\dfrac{5}{7}\right)^n+1}=\dfrac{4.0+7}{0+1}=7\)
\(\lim\dfrac{4^{n+1}+6^{n+2}}{5^n+8^n}=\lim\dfrac{8^n\left[4.\left(\dfrac{4}{8}\right)^n+36.\left(\dfrac{6}{8}\right)^n\right]}{8^n\left[\left(\dfrac{5}{8}\right)^n+1\right]}=\lim\dfrac{4.\left(\dfrac{4}{8}\right)^n+36\left(\dfrac{6}{8}\right)^n}{\left(\dfrac{5}{8}\right)^n+1}=\dfrac{0}{1}=0\)



Qua D kẻ đường thẳng song song AC cắt BA kéo dài tại E
\(\Rightarrow BE=2BA=2a\)
\(AC||DE\Rightarrow AC||\left(SDE\right)\Rightarrow d\left(AC;SD\right)=d\left(AC;\left(SDE\right)\right)=d\left(A;\left(SDE\right)\right)\)
\(AE=AD=a\Rightarrow\Delta ADE\) vuông cân tại A
Gọi I là trung điểm DE \(\Rightarrow AI\perp DE\Rightarrow DE\perp\left(SAI\right)\)
Trong mp (SAI), kẻ \(AJ\perp SI\Rightarrow AJ\perp\left(SDE\right)\Rightarrow AJ=d\left(A;\left(SDE\right)\right)\)
\(AI=\dfrac{AD}{2}=\dfrac{\sqrt{AE^2+AD^2}}{2}=\dfrac{a\sqrt{2}}{2}\)
\(\dfrac{1}{AJ^2}=\dfrac{1}{AI^2}+\dfrac{1}{SA^2}\Rightarrow AJ=\dfrac{AI.SA}{\sqrt{AI^2+SA^2}}=\dfrac{a\sqrt{3}}{3}\)
 Cần lắm cao nhân :V
Cần lắm cao nhân :V 


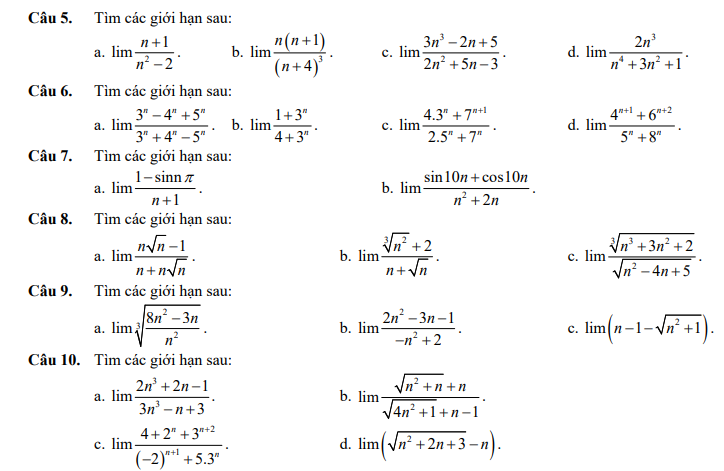






 câu 3 5c mn giúp em cần gấp lắm ạ
câu 3 5c mn giúp em cần gấp lắm ạ