K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Vẽ hình và giải chi tiết giúp mình nhé. Mình đang cần gấp.
15 tháng 10 2023
a: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
Do đó: BHCD là hình bình hành
b: BHCD là hình bình hành
=>BH//CDvà BD//CH
BH//CD
AC vuông góc BH
Do đó: CA vuông góc CD
=>ΔCAD vuông tại C
CH//BD
CH vuông góc AB
Do đó: BD vuông góc AB
=>ΔABD vuông tại B
c: \(\widehat{ABD}=\widehat{ACD}=90^0\)
=>ABDC là tứ giác nội tiếp đường tròn đường kính AD
=>ABDC nội tiếp (I)
=>IA=IB=ID=IC
NN
1
NT
2
XO
21 tháng 7 2021
2x(x - 5) - 2010(x - 5) = 0
<=> (2x - 2010)(x - 5) = 0
<=> \(\orbr{\begin{cases}2x-2010=0\\x-5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}2x=2010\\x=5\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1005\\x=5\end{cases}}\)
Vậy \(x\in\left\{1005;5\right\}\)là nghiệm phương trình
QA
21 tháng 7 2021
Trả lời:
\(2x\left(x-5\right)-2010\left(x-5\right)=0\)
\(\Leftrightarrow\left(2x-2010\right)\left(x-5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x-2010=0\\x-5=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=1005\\x=5\end{cases}}\)
Vậy x = 1005; x = 5 là nghiệm của pt.
BT
1
S
12 tháng 7 2018
\(G=x^2-4xy+5y^2+10x-22y+28\)
\(=\left(x^2-4xy+4y^2\right)+\left(y^2-2y+1\right)+10\left(x-2y\right)+25+2\)
\(=\left[\left(x-2y\right)^2+2.5\left(x-2y\right)+25\right]+\left(y-1\right)^2+2\)
\(=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\)
Vì \(\hept{\begin{cases}\left(x-2y+5\right)^2\ge0\\\left(y-1\right)^2\ge0\end{cases}\Rightarrow\left(x-2y+5\right)^2+\left(y-1\right)^2\ge0}\)
\(\Rightarrow G=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x-2y+5\right)^2=0\\\left(y-1\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x-2y+5=0\\y-1=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x+3=0\\y=1\end{cases}\Leftrightarrow}\hept{\begin{cases}x=-3\\y=1\end{cases}}}\)
Vậy Gmin = 2 khi x = -3, y = 1
KN
0
VD
0
31 tháng 12 2021
a: Xét tứ giác MNQP có
I là trung điểm của NP
I là trung điểm của MQ
Do đó: MNQP là hình bình hành
mà MQ=NP
nên MNQP là hình chữ nhật
19 tháng 11 2021
\(a,=\dfrac{2y\left(3x-1\right)^2}{3x^2}\\ b,=\dfrac{\left(3x+2-x-2\right)\left(3x+2+x+2\right)}{x^2\left(x-1\right)}\\ =\dfrac{2x\left(4x+4\right)}{x^2\left(x-1\right)}=\dfrac{8\left(x+1\right)}{x\left(x-1\right)}\\ c,=\dfrac{x^2+3x+4x+12}{x^2+2x+3x+6}\\ =\dfrac{\left(x+3\right)\left(x+4\right)}{\left(x+2\right)\left(x+3\right)}=\dfrac{x+4}{x+2}\)
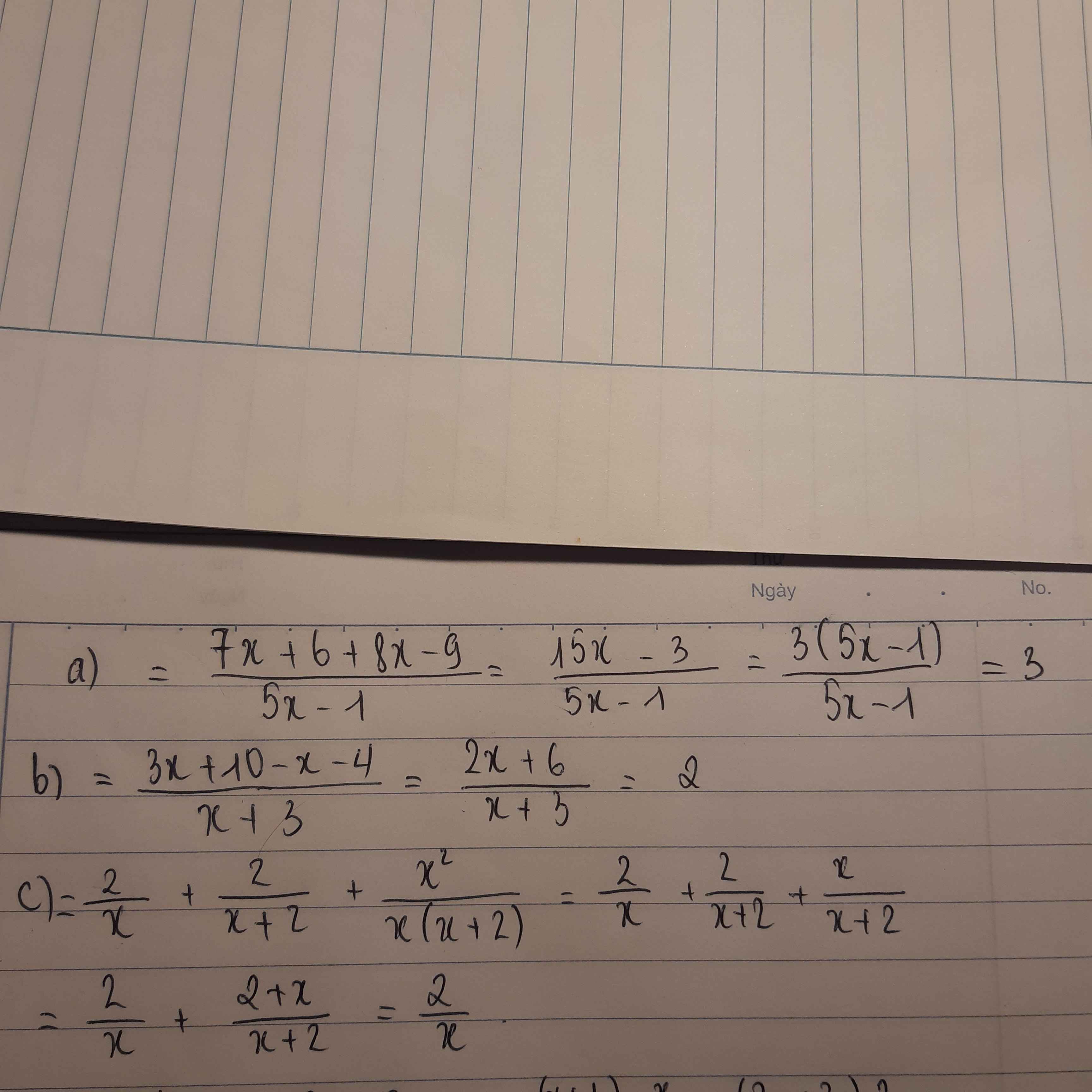
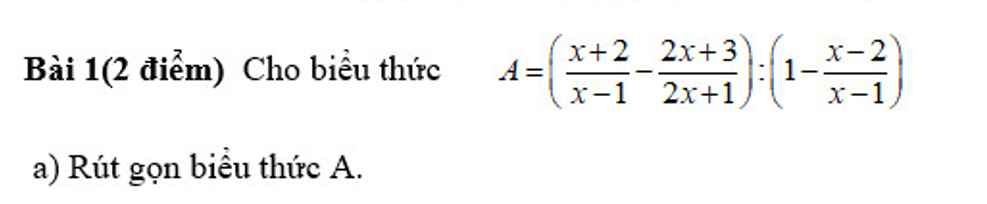
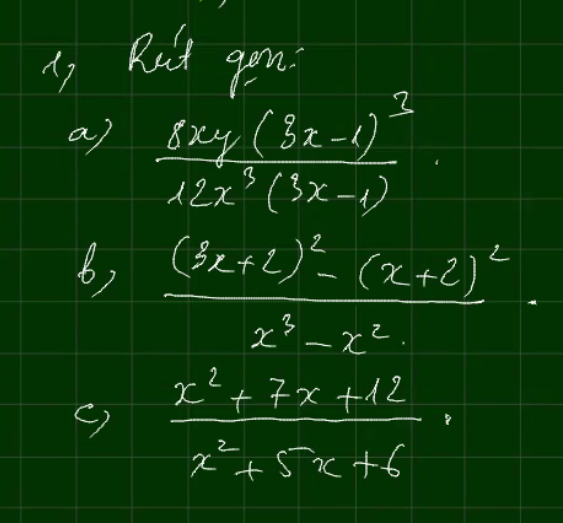
Câu 1: D
Câu 2: D
Câu 3: B
Câu 4: C