K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 10 2021
\(c,\Rightarrow\left|x-\dfrac{1}{9}\right|=-\dfrac{4}{5}\\ \Rightarrow x\in\varnothing\left(\left|x-\dfrac{1}{9}\right|\ge0>-\dfrac{4}{5}\right)\\ d,\Rightarrow\left\{{}\begin{matrix}3x-2=0\\4y-7=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{2}{3}\\y=\dfrac{7}{4}\end{matrix}\right.\\ e,\Rightarrow\left\{{}\begin{matrix}2x+1=0\\x-y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\x=y=-\dfrac{1}{2}\end{matrix}\right.\Rightarrow x=y=-\dfrac{1}{2}\)
S
4 tháng 3 2023
Ta có:
\(\dfrac{x}{10}=\dfrac{y}{5}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}\) \(\left(1\right)\)
\(\dfrac{y}{2}=\dfrac{z}{3}\)
\(\Rightarrow\dfrac{y}{10}=\dfrac{z}{15}\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{z}{15}\)
Lại có:
\(\dfrac{z}{15}=\dfrac{4z}{60}\)
Áp dụng tính chất của dãy tỉ số bằng nhau,ta có:
\(\dfrac{x}{20}=\dfrac{y}{10}=\dfrac{4z}{60}=\dfrac{x+4z}{20+60}=\dfrac{240}{80}=3\)
\(\Rightarrow x=3\cdot20=60\)
\(y=3\cdot10=30\)
\(z=3\cdot15=45\)
TH
4 tháng 3 2020
d, cm tam giác EMK = tam giác FMH (c-g-c)
=> EM = MF => M là trđ của EF
Cm tam giác BEH = tam giác FHE (c-g-c) => BH // EF => EF _|_ AM
=> tam giác AEF cân tại A
không hiểu chỗ nào thì hỏi
4 tháng 3 2020
a) Xét Δ B H M ; Δ C K M ΔBHM;ΔCKM có :
ˆ B H M = ˆ C K M ( = 90 o − g t )
BHM^=CKM^(=90o−gt)
B M = M C ( g t ) BM=MC(gt) ˆ H M B = ˆ K M C HMB^=KMC^ (đối đỉnh)
=> Δ B H M = Δ C K M ΔBHM=ΔCKM (cạnh huyền - góc nhọn)
=> ˆ H B M = ˆ K C M HBM^=KCM^ (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=> BH // KC ( đ p c m ) BH // KC(đpcm)
Và từ Δ B H M = Δ C K M ΔBHM=ΔCKM (cmt)
=> B H = C K BH=CK (2 cạnh tương ứng)
b) Xét Δ H M C ; Δ K M B ΔHMC;ΔKMB có :
B M = M C ( g t )
BM=MC(gt) ˆ H M C = ˆ K M B HMC^=KMB^ (đối đỉnh)
H M = M K HM=MK (do Δ B H M = Δ C K M ΔBHM=ΔCKM -cmt)
=> Δ H M C ; Δ K M B ΔHMC;ΔKMB
=> Δ H M C = Δ K M B ΔHMC=ΔKMB (c.g.c)
=> ˆ H C M = ˆ K B M HCM^=KBM^ (2 góc tương ứng)
Mà : 2 góc này ở vị trí so le trong
=> BK // CH ( đ p c m ) BK // CH (đpcm)
Có : Δ H M C = Δ K M B ΔHMC=ΔKMB (cmt)
=> B K = C H BK=CH (2 cạnh tương ứng)
c) Ta có : { H F = F C B E = E K {HF=FCBE=EK (gt)
Mà : B K = H C ( c m t ) BK=HC(cmt)
=> H F = F C = B E = E K HF=FC=BE=EK
Xét Δ B E M ; Δ F C M ΔBEM;ΔFCM có :
B M = M C ( g t ) BM=MC(gt) ˆ M B E = ˆ M C F ( s l t )
MBE^=MCF^(slt) B E = F C ( c m t ) BE=FC(cmt)
=> Δ B E M = Δ F C M ( c . g . c ) ΔBEM=ΔFCM(c.g.c)
=> E M = F M EM=FM(2 cạnh tương ứng)
=> M Là trung điểm của EF Do đó : E, ,M, F thẳng hàng
6 tháng 1 2022
Xét tứ giác GHKI có
GH//KI
GH=KI
Do đó: GHKI là hình bình hành
Suy ra: GI=HK
LN
1
6 tháng 7 2022
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó:ΔABH=ΔACH
b: Xét ΔDBC có
DH là đường cao
DH là đường trung tuyến
Do đó:ΔDBC cân tại D
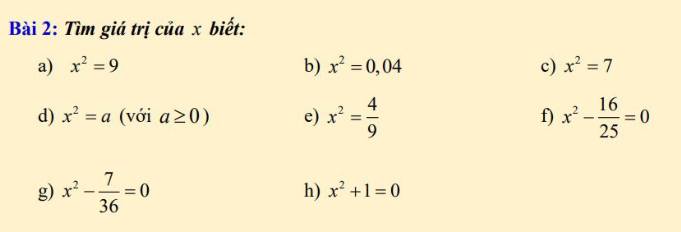
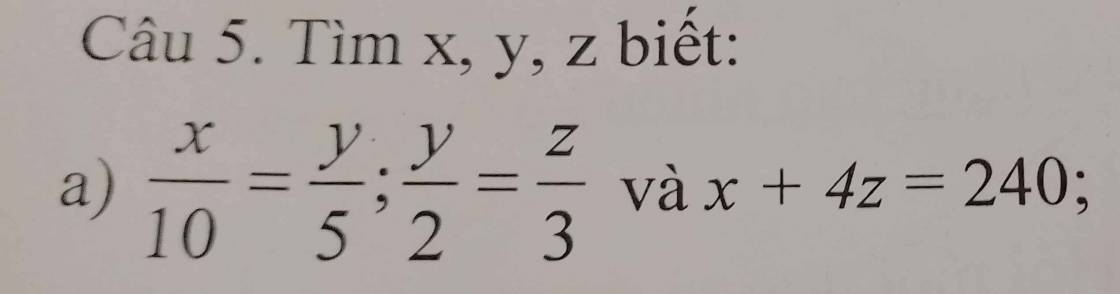
d) \(x^2=a\left(a\ge0\right)\)
\(\Rightarrow x=\sqrt{a}\)
e) \(x^2=\dfrac{4}{9}\)
\(\Rightarrow x^2=\left(\pm\dfrac{2}{3}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
f) \(x^2-\dfrac{16}{25}=0\)
\(\Rightarrow x^2=\dfrac{16}{25}\)
\(\Rightarrow x^2=\left(\pm\dfrac{4}{5}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)
g) \(x^2-\dfrac{7}{36}=0\)
\(\Rightarrow x^2=\dfrac{7}{36}\)
\(\Rightarrow x^2=\left(\pm\sqrt{\dfrac{7}{36}}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{7}{36}}\\x=-\sqrt{\dfrac{7}{36}}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{7}}{6}\\x=-\dfrac{\sqrt{7}}{6}\end{matrix}\right.\)
h) Ta có: \(x^2\ge0\forall x\)
\(\Rightarrow x^2+1\ge1>0\forall x\)
mà \(x^2+1=0\)
nên không tìm được giá trị nào của x thoả mãn đề bài.