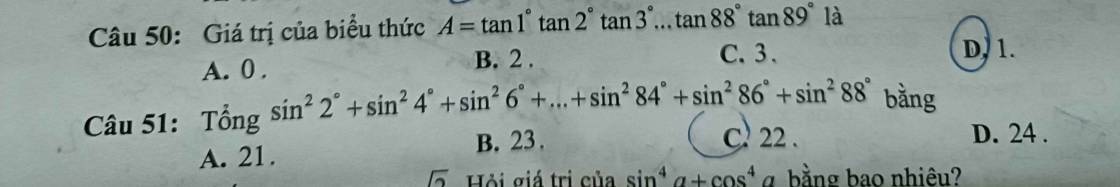Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(sin^2x=\left(sinx\right)^2\ne sin\left(x^2\right)\)
1 cái là bình phương của cả hàm sin, 1 cái chỉ là bình phương của góc
Cách giải bài này: suy nghĩ đầu tiên: hạ bậc.
Đầu tiên chắc chắn là phải biến đổi \(-sin^2a-sin^2b\) (phần \(sin^2\left(a+b\right)\) nếu áp dụng \(sin^2\left(a+b\right)=\left(sina.cosb+cosa.sinb\right)^2\) thì khai triển ra sẽ rất thảm họa nên cứ để đó từ từ tính sau)
\(-sin^2a-sin^2b=-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2a\right)-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2b\right)\) (công thức hạ bậc)
\(=-1+\dfrac{1}{2}\left(cos2a+cos2b\right)=-1+cos\left(a+b\right)cos\left(a-b\right)\) (công thức biến tổng thành tích)
Thấy xuất hiện góc \(\left(a+b\right)\) giống góc của \(sin^2\left(a+b\right)\) rồi, nhưng của hàm cos, vậy thì đơn giản hãy biến \(sin^2\left(a+b\right)\) thành hàm cos bằng công thức cơ bản: \(sin^2\left(a+b\right)=1-cos^2\left(a+b\right)\)
Do đó, chắc chắn bài toán sẽ được giải quyết như sau:
\(A=1-cos^2\left(a+b\right)-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2a\right)-\left(\dfrac{1}{2}-\dfrac{1}{2}cos2b\right)\)
\(A=-cos^2\left(a+b\right)+\dfrac{1}{2}\left(cos2a+cos2b\right)\)
\(A=-cos^2\left(a+b\right)+cos\left(a+b\right)cos\left(a-b\right)\)
\(=cos\left(a+b\right)\left[cos\left(a-b\right)-cos\left(a+b\right)\right]\)
\(=2sina.sinb.cos\left(a+b\right)\)
(Sử dụng biến tổng thành tích: \(cosx-cosy=-2sin\dfrac{x+y}{2}sin\dfrac{x-y}{2}\)
Thì: \(cos\left(a-b\right)-cos\left(a+b\right)=-2sin\dfrac{a-b+a+b}{2}sin\dfrac{a-b-a-b}{2}=-2sina.sin\left(-b\right)=2sina.sinb\)



5:
a: (C): x^2-4x+4+y^2-2y+1-9=0
=>(x-2)^2+(y-1)^2=9
=>R=3; I(2;1)
b: vecto IM=(-1;3)
=>(d) có VTPT là (-1;3)
Phương trình d là;
-1(x-1)+3(y-4)=0
=>-x+1+3y-12=0
=>-x+3y-11=0

Câu 50 thì bạn nhóm cặp lại tan1*tan89*tan2*tan88*...*tan45
thì bạn sẽ thấy là tan1*tan89=tan2*tan88=...=tan45=1
=>D
Câu 51 thì bạn nhóm cặp lại \(sin^288^0;sin^22^0\); sin2860 và sin240;...;sin244 độ và sin2 46 độ thì bạn sẽ thấy từng cặp đó có tổng bằng 1
Và có 22 cặp như vậy nên đáp án là C


1.1
Pt có 2 nghiệm trái dấu và tổng 2 nghiệm bằng -3 khi:
\(\left\{{}\begin{matrix}ac< 0\\x_1+x_2=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\left(m+2\right)< 0\\\dfrac{2m+1}{m+2}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -2\\m=-\dfrac{7}{5}\end{matrix}\right.\)
\(\Rightarrow\) Không tồn tại m thỏa mãn
b.
Pt có nghiệm kép khi:
\(\left\{{}\begin{matrix}m+2\ne0\\\Delta=\left(2m+1\right)^2-8\left(m+2\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m^2-4m-15=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=\dfrac{5}{2}\\m=-\dfrac{3}{2}\end{matrix}\right.\)