CN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
15 tháng 2 2022
Ủa r siêng năng may vượt mức chi r để hs phải đi tính zị trời😤
AT
3 tháng 7 2021
Bài 1:1) \(10+2\sqrt{10}=\sqrt{10}\left(2+\sqrt{10}\right)\)
2) \(7+3\sqrt{7}=\sqrt{7}\left(3+\sqrt{7}\right)\)
các câu 3,4,5 bạn làm tương tự như 2 câu trên
6) \(3a\sqrt{b}+3b\sqrt{a}=3\sqrt{ab}\left(\sqrt{a}+\sqrt{b}\right)\)
7) \(a^2-2a\sqrt{2}+2=a^2-2a\sqrt{2}+\left(\sqrt{2}\right)^2=\left(a-\sqrt{2}\right)^2\)
8) \(b-4=\left(\sqrt{b}\right)^2-2^2=\left(\sqrt{b}-2\right)\left(\sqrt{b}+2\right)\)
Bài 2: 1) \(\dfrac{\left(2-\sqrt{a}\right)^2-\left(\sqrt{a}+3\right)^2}{2a+\sqrt{a}}\left(a>0\right)\)
\(=\dfrac{\left(2-\sqrt{a}-\sqrt{a}-3\right)\left(2-\sqrt{a}+\sqrt{a}+3\right)}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=\dfrac{\left(-2\sqrt{a}-1\right).5}{\sqrt{a}\left(2\sqrt{a}+1\right)}=-\dfrac{5}{\sqrt{a}}\)
3) \(\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{\sqrt{a}-2}\left(a\ge0,a\ne4\right)\)
\(=\dfrac{\left(\sqrt{a}+2\right)^2}{\sqrt{a}+2}+\dfrac{\left(2-\sqrt{a}\right)\left(2+\sqrt{a}\right)}{\sqrt{a}-2}=\sqrt{a}+2-\left(2+\sqrt{a}\right)=0\)
4) \(\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\left(a\ge0,a\ne1\right)\)
\(=\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a}-1}\right)\left(1-\dfrac{\sqrt{a}\left(\sqrt{a}+1\right)}{1+\sqrt{a}}\right)\)
\(=\left(1-\sqrt{a}\right)\left(1-\sqrt{a}\right)=\left(1-\sqrt{a}\right)^2=a-2\sqrt{a}+1\)
mấy câu còn lại bạn làm tương tự
3 tháng 7 2021
Bài 1:
1) \(10+2\sqrt{10}=2\sqrt{5}\left(\sqrt{5}+\sqrt{2}\right)\)
2) \(7+3\sqrt{7}=\sqrt{7}\left(\sqrt{7}+3\right)\)
3) \(5\sqrt{7}-7\sqrt{5}=\sqrt{35}\left(\sqrt{5}-\sqrt{7}\right)\)
4) \(4\sqrt{3}-2\sqrt{6}=2\sqrt{6}\left(\sqrt{2}-\sqrt{1}\right)\)
5) \(6\sqrt{6}-2\sqrt{12}+3\sqrt{2}\)
\(=\sqrt{216}-\sqrt{48}+\sqrt{18}\)
\(=\sqrt{6}\left(6-2\sqrt{2}+\sqrt{3}\right)\)
6) \(3a\sqrt{6}+36\sqrt{a}\)
\(=3\sqrt{a}\left(\sqrt{6a}+12\right)\)
\(=3\sqrt{6a}\left(\sqrt{a}+2\sqrt{6}\right)\)
7) \(a^2-2a\sqrt{2}+2=\left(a-\sqrt{2}\right)^2\)
8) \(b-4=\left(\sqrt{b}-2\right)\left(\sqrt{b}+2\right)\)
Bài 2:
a) Ta có: \(\dfrac{\left(2-\sqrt{a}\right)^2-\left(\sqrt{a}+3\right)^2}{2a+\sqrt{a}}\)
\(=\dfrac{a-4\sqrt{a}+4-a-6\sqrt{a}-9}{2a+\sqrt{a}}\)
\(=\dfrac{-10\sqrt{a}-5}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=\dfrac{-5\left(2\sqrt{a}+1\right)}{\sqrt{a}\left(2\sqrt{a}+1\right)}\)
\(=-\dfrac{5}{\sqrt{a}}\)
4) Ta có: \(\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)\left(1-\dfrac{a+\sqrt{a}}{1+\sqrt{a}}\right)\)
\(=\left(1-\sqrt{a}\right)\left(1-\sqrt{a}\right)\)
\(=a-2\sqrt{a}+1\)
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
Gọi O là tâm đường tròn \(\Rightarrow\) O là trung điểm BC
\(\stackrel\frown{BE}=\stackrel\frown{ED}=\stackrel\frown{DC}\Rightarrow\widehat{BOE}=\widehat{EOD}=\widehat{DOC}=\dfrac{180^0}{3}=60^0\)
Mà \(OD=OE=R\Rightarrow\Delta ODE\) đều
\(\Rightarrow ED=R\)
\(BN=NM=MC=\dfrac{2R}{3}\Rightarrow\dfrac{NM}{ED}=\dfrac{2}{3}\)
\(\stackrel\frown{BE}=\stackrel\frown{DC}\Rightarrow ED||BC\)
Áp dụng định lý talet:
\(\dfrac{AN}{AE}=\dfrac{MN}{ED}=\dfrac{2}{3}\Rightarrow\dfrac{EN}{AN}=\dfrac{1}{2}\)
\(\dfrac{ON}{BN}=\dfrac{OB-BN}{BN}=\dfrac{R-\dfrac{2R}{3}}{\dfrac{2R}{3}}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{EN}{AN}=\dfrac{ON}{BN}=\dfrac{1}{2}\) và \(\widehat{ENO}=\widehat{ANB}\) (đối đỉnh)
\(\Rightarrow\Delta ENO\sim ANB\left(c.g.c\right)\)
\(\Rightarrow\widehat{NBA}=\widehat{NOE}=60^0\)
Hoàn toàn tương tự, ta có \(\Delta MDO\sim\Delta MAC\Rightarrow\widehat{MCA}=\widehat{MOD}=60^0\)
\(\Rightarrow\Delta ABC\) đều
L
0
2 tháng 3 2023
Sửa đề: Trên dây CB
góc FCP=1/2*sd cung CB
góc FPC=góc EDB=90 độ-góc ABC
=90 độ-1/2*sđ cung AC
=góc CAB=1/2*sđ cung CB
=>góc FCP=góc FPC
=>ΔFPC cân tại F
17 tháng 1 2023
Bài 1:
a: Khi x=16 thì \(A=\dfrac{4+1}{4-1}=\dfrac{5}{3}\)
b: P=A*B
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\cdot\dfrac{x+2\sqrt{x}+1-3\sqrt{x}-1}{x-1}\)
\(=\dfrac{1}{\left(\sqrt{x}-1\right)^2}\cdot\sqrt{x}\left(\sqrt{x}-1\right)=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
c: Để |P-2|=2-P thì P-2<0
=>(căn x-2căn x+2)/(căn x-1)<0
=>(căn x-2)/(căn x-1)>0
=>x>4 hoặc 0<x<1
KV
4 tháng 11 2023
Bài 22
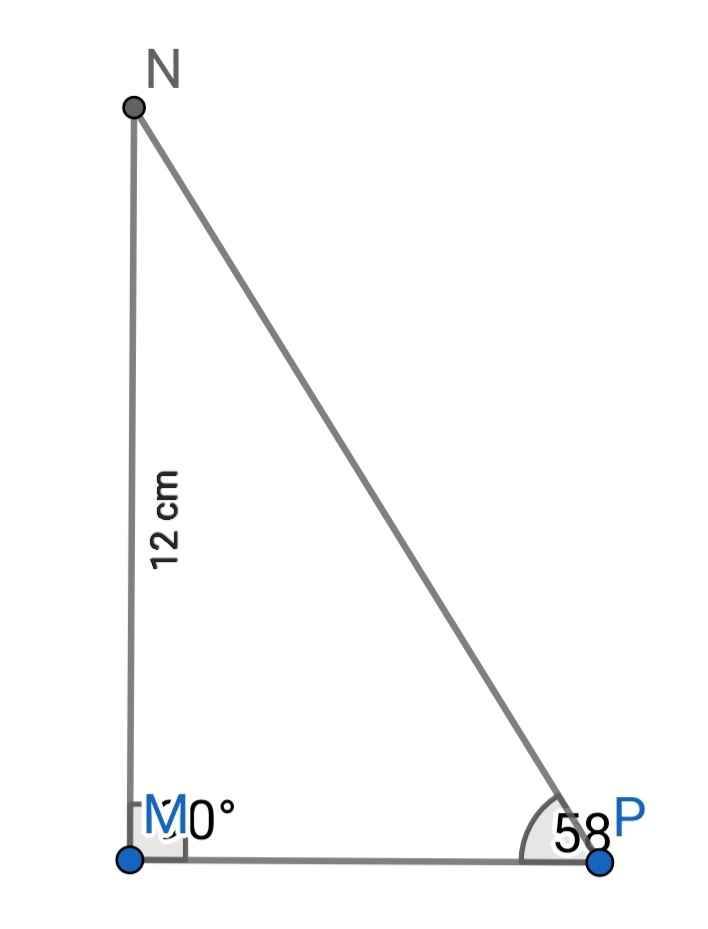Ta có:
∠P + ∠N = 90⁰
⇒ ∠N = 90⁰ - ∠P
= 90⁰ - 58⁰
= 32⁰
sin P = MN/NP
⇒ NP = MN : sin P
= 12 : sin 58⁰
≈ 14,2 (cm)
tan P = MN/MP
⇒ MP = MN : tan P
= 12 : tan 58⁰
≈ 7,5 (cm)
4 tháng 9 2021
f: Vì (d)//y=2x-3 nên a=2
Vậy: (d): y=2x+b
Thay x=0 và y=2 vào (d), ta được:
b=2
Bài 1:
a: \(A=\dfrac{2\sqrt{x}-9+2x-4\sqrt{x}+\sqrt{x}-2-x+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x-\sqrt{x}-2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-3}\)