Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A.
Do ABCDE là ngũ giác đều nội tiếp đường tròn (O) nên:
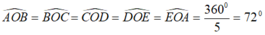
Suy ra, sđ A B ⏜ = 72 °

vẽ đường tròn ngoại tiếp ngũ giác đều ABCDE
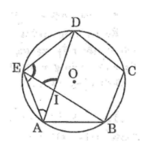

Suy ra tam giác DEI cân tại D ⇒ DI = DE
Mà DE =AE
Nên DI = AE (7)
Từ (4) và (7) suy ra: D I 2 = AI.AD

Hình vẽ: Gọi gia điểm của AC và BD là F.
CM AEDF là hình bình hành từ đó suy ra SADE=SADF=1.SADE=SADF=1.
Đặt SBFC=x⇒SCDF=1−x.SBFC=x⇒SCDF=1−x.
CM ΔBFCΔBFC đồng dạng với ΔDFA.ΔDFA.
Tìm được SCDF=−1+√52.SCDF=−1+52.
⇒So=3.618033989dm2⇒So=3.618033989dm2.
Giả sử ngũ giác \(ABCDE\) thỏa mãn đk bài toán
Xét \(\Delta BCD\)Và \(ECD\)và \(S_{BCD}=S_{ECD}\)đáy \(CD\)chung, các đường cao hạ từ \(B\)và \(E\)xuống \(CD\) bằng nhau => \(EB\) ∗ \(CD\),Tương tự \(AC\)//\(ED\) ,\(BD\) ∗\(AE\), \(CE\) ∗ \(AB\), \(DA\) ∗ \(BC\)
Gọi \(I\) \(=EC\)∩\(BC\)=> \(ABIE\)là hình bình hành
=> \(S_{IBE}=S_{ABE}=1\)Đặt\(S_{ICD}=x< 1\)
=> SIBC = SBCD - SICD = 1-x = SECD - SICD = SIED
Lại có: \(\orbr{\begin{cases}S_{ICD}=IC=S_{IBC}\\S_{IDE}=IE=S_{IBE}\end{cases}}\)Hay \(\orbr{\begin{cases}x\\1-x\end{cases}}\)\(=\orbr{\begin{cases}1-x\\1\end{cases}}\)
=> x2-3x+ 1 = 0 => x =\(\frac{3+5}{2}\)Do x<1 => x=\(\frac{3-5}{2}\)
Vậy \(S_{IBE}=\frac{5-1}{2}\)
Do đó SABCDE = SEAB + SEBI + SBCD + SIED
\(=3+\frac{5-1}{2}=\frac{5+5}{2}=5\)


1/2 !! >_<
làm zõ hộ đi