Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích hình vuông \(ABCD\) : \(\dfrac{1}{2}\times4\times4=8\left(cm^2\right)\)
Diện tích \(\Delta DKN\) : \(\dfrac{1}{2}\times4\times4=8\left(cm^2\right)\)
Diện tích phần còn lại là: \(36-\left(8+8\right)=20\left(cm^2\right)\)
Trong \(\Delta\) vuông \(AEN\) ta có:
\(EN^2=AN^2+AE^2=4+4=8\)
\(EN=\sqrt{8}=2\sqrt{2}\left(cm\right)\)
Trong \(\Delta\) vuông \(BHE\) ta có:
\(EH^2=BE^2+BH^2=16+16=32\)
\(EH=\sqrt{32}=4\sqrt{2}\left(cm\right)\)
\(S_{ENKH}=2\sqrt{2}\times4\sqrt{2}=16\left(cm^2\right)\)
Nối đường chéo \(BD\). Théo tính chất đường thẳng song song cách đều ta có hình chữ nhật \(ENKH\) chia thành bốn phần bằng nhau nên \(S_{PQRS}\) chiếm 2 phần bằng \(8cm^2\) .
\(S_{AEPSN}=S_{AEN}+S_{EPSN}=2+\dfrac{16}{4}=6\left(cm^2\right)\)
Vậy............
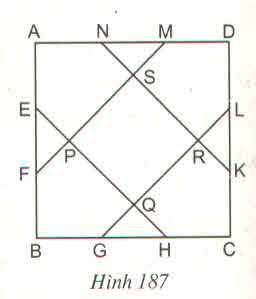


Diện tích hình vuông ABCD bằng 6.6 = 36 ( c m 2 )
Diện tích △ BEH bằng 1/2 .4.4 = 8 ( c m 2 )
Diện tích △ DKN bằng 1/2 .4.4 = 8 ( c m 2 )
Diện tích phần còn lại là: 36 - (8 + 8) = 20 ( c m 2 )
Trong tam giác vuông AEN, ta có:
E N 2 = A N 2 + A E 2 = 4 + 4 = 8 ⇒ EN = 2 2 (cm)
Trong tam giác vuông BHE, ta có:
E H 2 = B E 2 + B H 2 = 16 + 16 = 32 ⇒ EH = 4 2 (cm)
Diện tích hình chữ nhật ENKH bằng: 2 2 . 4 2 = 16 ( c m 2 )
Nối đường chéo BD. Theo tính chất đường thẳng song song cách đều ta có hình chữ nhật ENKH được chia thành 4 phần bằng nhau nên diện tích tứ giác PQRS chiếm 2 phần bằng 8 c m 2
Diện tích △ AEN bằng 1/2 .2.2 = 2 ( c m 2 )
Vậy S A E P S N = S A E N + S E P S N = 2 + 16/4 = 6 ( c m 2 )