K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 3 2022
a: Xét ΔSBM và ΔSNB có
\(\widehat{SBM}=\widehat{SNB}\)
\(\widehat{BSM}\) chung
Do đó: ΔSBM\(\sim\)ΔSNB
Suy ra: SB/SN=SM/SB
hay \(SB^2=SM\cdot SN\)
b: Xét (O) có
SA là tiếp tuyến
SB là tiếp tuyến
Do đó: SA=SB
mà OA=OB
nên SO là đường trung trực của AB
=>SO⊥AB
Xét ΔOBS vuông tại B có BH là đường cao
nên \(SH\cdot SO=SB^2=SM\cdot SN\)
2 tháng 8 2021
a) Ta có: \(\dfrac{3}{2}\sqrt{12}+\sqrt{75}-\sqrt{300}+\sqrt{27}\)
\(=3\sqrt{3}+5\sqrt{3}-10\sqrt{3}+3\sqrt{3}\)
\(=\sqrt{3}\)
b) Ta có: \(\sqrt{14-6\sqrt{5}}+\sqrt{9-4\sqrt{5}}\)
\(=3-\sqrt{5}+\sqrt{5}-2\)
=1
12 tháng 11 2021
1 \(\Leftrightarrow\left\{{}\begin{matrix}15x-5y=40\\2x+5y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3x-8=1\end{matrix}\right.\)
TH
1
G
6 tháng 4 2022
Ta có 1ml = 1cm3
Vậy thể tích của lọ đựng dung dịch đó là 100 cm3
Diện tích trong của đáy lọ là:
Ta có: V = S đáy * h => S đáy = V : h = 100 : 12.5 = 8 (cm2)
VD
1
22 tháng 1
Câu 2:
a:
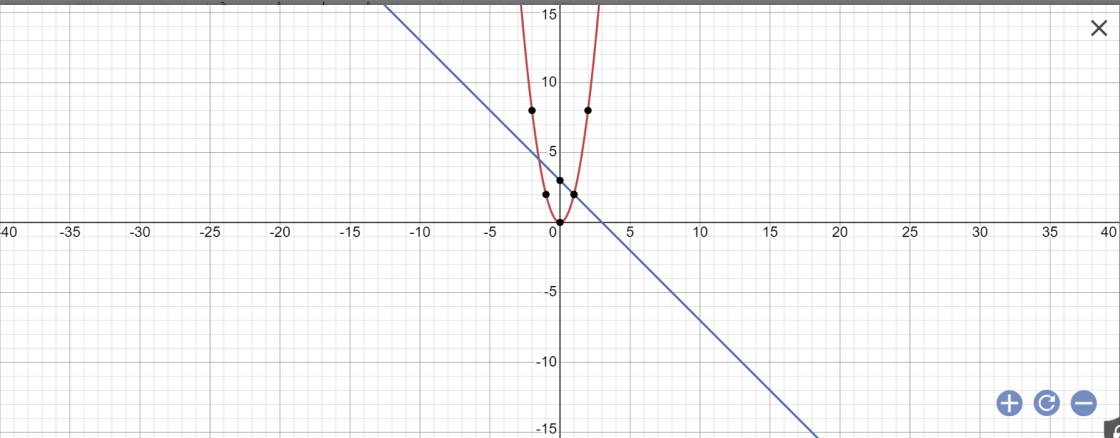
b: phương trình hoành độ giao điểm là:
\(2x^2=-x+3\)
=>\(2x^2+x-3=0\)
=>\(2x^2+3x-2x-3=0\)
=>(2x+3)(x-1)=0
=>\(\left[{}\begin{matrix}2x+3=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=1\end{matrix}\right.\)
Thay x=-3/2 vào (P), ta được:
\(y=2\cdot\left(-\dfrac{3}{2}\right)^2=2\cdot\dfrac{9}{4}=\dfrac{9}{2}\)
Thay x=1 vào (P), ta được:
\(y=2\cdot1^2=2\)
Vậy: (P) cắt (d) tại hai điểm là \(A\left(-\dfrac{3}{2};\dfrac{9}{2}\right);B\left(1;2\right)\)