Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{1}{\sqrt{3}-\sqrt{2}}+\dfrac{1}{\sqrt{3}+\sqrt{2}}-\dfrac{3-\sqrt{3}}{\sqrt{3}-1}\)
\(=\dfrac{\sqrt{3}+\sqrt{2}}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)}+\dfrac{\sqrt{3}-\sqrt{2}}{\left(\sqrt{3}+\sqrt{2}\right)\left(\sqrt{3}-\sqrt{2}\right)}-\dfrac{\sqrt{3}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}\)
\(=\dfrac{\sqrt{3}+\sqrt{2}}{3-2}+\dfrac{\sqrt{3}-\sqrt{2}}{3-2}-\sqrt{3}\)
\(=\sqrt{3}+\sqrt{2}+\sqrt{3}-\sqrt{2}-\sqrt{3}\)
\(=2\sqrt{3}-\sqrt{3}\)
\(=\sqrt{3}\)

Lời giải:
$\frac{1}{x}+\frac{1}{y}+\frac{2}{x+y}=\frac{x+y}{xy}+\frac{2}{x+y}$
$=x+y+\frac{2}{x+y}$
$=\frac{x+y}{2}+\frac{x+y}{2}+\frac{2}{x+y}$
$\geq \frac{x+y}{2}+2\sqrt{\frac{x+y}{2}.\frac{2}{x+y}}$ (áp dụng BDT Cô-si)
$\geq \frac{2\sqrt{xy}}{2}+2=\frac{2}{2}+2=3$
Vậy ta có đpcm
Dấu "=" xảy ra khi $x=y=1$

\(=\dfrac{\sqrt{a}+2+\sqrt{a}-2}{a-4}:\dfrac{\sqrt{a}+2-2}{\sqrt{a}+2}\)
\(=\dfrac{2\sqrt{a}}{a-4}\cdot\dfrac{\sqrt{a}+2}{\sqrt{a}}=\dfrac{2}{\sqrt{a}-2}\)

câu 1:
đường thẳng (d) song song với đường thẳng y=3x+1 khi a=3
vậy hệ số góc của đường thẳng (d) song song với đường thẳng y=3x+1 là 3
câu 2:
vì góc tạo bởi đường thẳng (d):y=ax+b(a≠0) với trục Ox là 30o nên
\(a=\tan30^o=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
vậy hệ số góc của đường thẳng (d) tạo với trục Ox là\(\dfrac{\sqrt{3}}{3}\)

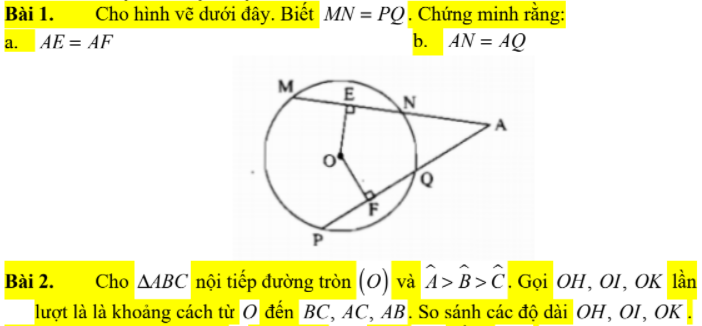
Bài 2:
Ta có: \(\widehat{A}>\widehat{B}>\widehat{C}\)
nên BC>AC>AB
hay OH<OI<OK


Đề ko rõ ràng \(\sqrt{x^2}+x+\dfrac{1}{4}\) hay \(\sqrt{x^2+x+\dfrac{1}{4}}\)??

a: \(f\left(\dfrac{1}{2}\right)=\dfrac{1}{4}+\dfrac{1}{2}-2=-\dfrac{5}{4}\)
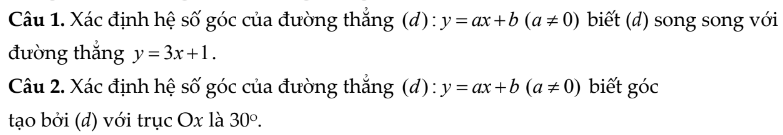

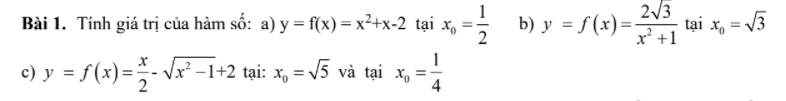 , mình đang cần để nộp ạ. Cảm ơn mn nhiều.
, mình đang cần để nộp ạ. Cảm ơn mn nhiều.