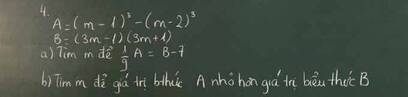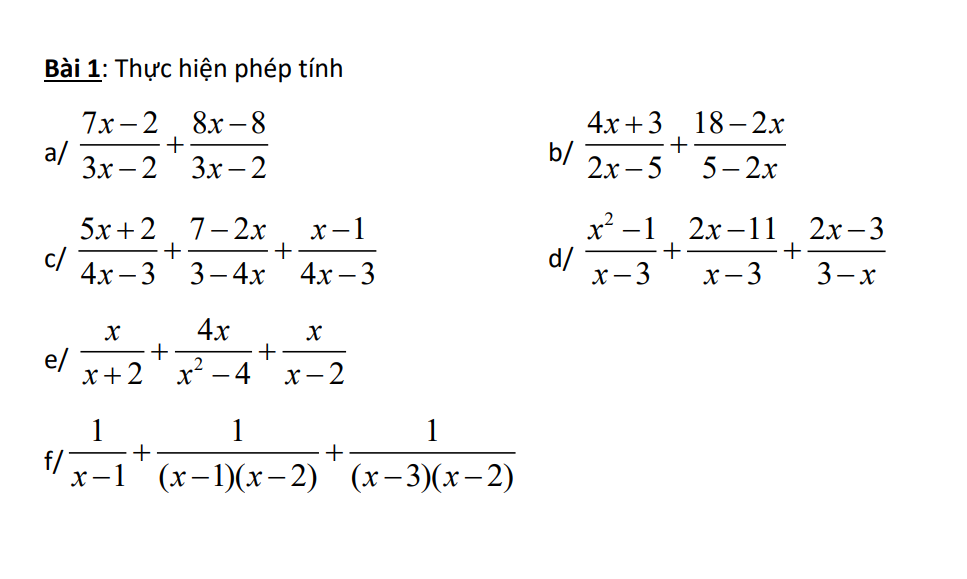các bạn ơi giúp mình với pls cần gấp
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 10 2021
Bài 5:
a: \(\left(x+3\right)\left(x-3\right)-\left(x-2\right)\left(x+5\right)=6\)
\(\Leftrightarrow x^2-9-x^2-3x+10=6\)
\(\Leftrightarrow-3x=5\)
hay \(x=-\dfrac{5}{3}\)
MK
1
YN
20 tháng 6 2022
\(a)\)
\(A=\left(m-1\right)^3-\left(m-2\right)^3\)
\(=\left(m^3-3m^2+3m-1\right)-\left(m^3-6m^2+12m-8\right)\)
\(=m^3-3m^2+3m-1-m^3+6m^2-12m+8\)
\(=3m^2-9m+7\)
\(B=\left(3m-1\right)\left(3m+1\right)\)
\(=9m^2-1\)
\(\dfrac{1}{9}A=B-7\)
\(\Rightarrow\dfrac{1}{9}\left(3m^2-9m+7\right)=9m^2-1-7\)
\(\Rightarrow3m^2-9m+7=81m^2-72\)
\(\Rightarrow78m^2+9m-79=0\)
\(\Rightarrow m=\dfrac{-9\pm\sqrt{24729}}{156}\)
\(b)\)
\(A< B\)
\(\Rightarrow3m^2-9m+7< 9m^2-1\)
\(\Rightarrow6m^2+9m-8>0\)
\(\Rightarrow\left[{}\begin{matrix}m>\dfrac{-9+\sqrt{273}}{12}\\m< \dfrac{-9-\sqrt{273}}{12}\end{matrix}\right.\)
17 tháng 9 2021
Gọi E là giao điểm của AC và BD.
∆ECD có ∠C1 = ∠D1 (do ∠ACD = ∠BDC) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự ∆EAB cân tại A suy ra: EA = EB (2)
Từ (1) và (2) ta có: EA + EC = EB + ED ⇒ AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.4
14 tháng 12 2021
\(a,=\dfrac{7x-2+8x-8}{3x-2}=\dfrac{5\left(3x-2\right)}{3x-2}=5\\ b,=\dfrac{4x+3+2x-18}{2x-5}=\dfrac{3\left(2x-5\right)}{2x-5}=3\\ c,=\dfrac{5x+2+2x-7+x-1}{4x-3}=\dfrac{2\left(4x-3\right)}{4x-3}=2\\ d,=\dfrac{x^2-1+2x-11+3-2x}{x-3}=\dfrac{\left(x-3\right)\left(x+3\right)}{x-3}=x+3\\ e,=\dfrac{x^2-2x+4x+x^2+2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{2x}{x-2}\)
\(f,=\dfrac{x^2-5x+6+x-3+x-1}{\left(x-1\right)\left(x-2\right)\left(x-3\right)}=\dfrac{\left(x-1\right)\left(x-2\right)}{\left(x-1\right)\left(x-2\right)\left(x-3\right)}=\dfrac{1}{x-3}\)