Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

sgk toán 8 tập 1
Bài 74. Hai đường chéo của một hình thoi bằng 8cm8cm và 10cm10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
(A) 6cm6cm; (B) √41cm41cm
(C) √164cm164cm (D) 9cm9cm ?
Bài giải:
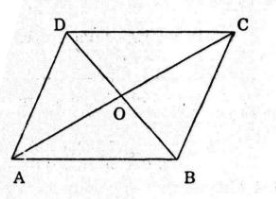
Xét bài toán tổng quát:
ABCDABCD là hình thoi, OO là giao điểm hai đường chéo.
Theo tính của hình thoi hai đường chéo của hình thoi vuông góc và cắt nhau tại trung điểm mỗi đường.
Áp dụng định lí Pytago vào tam giác vuông ABOABO ta có:
AB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=√(12AC)2+(12BD)2=√42+52=√41cmAB2=OA2+OB2=(12AC)2+(12BD)2⇒AB=(12AC)2+(12BD)2=42+52=41cm
Vậy (B) đúng.
Bài 79.
a) Một hình vuông có cạnh bằng 3cm3cm. Đường chéo của hình vuông đó bằng 6cm6cm, √18cm18cm, 5cm5cm hay 4cm4cm ?
b) Đường chéo của một hình vuông bằng 2dm2dm. Cạnh cảu hình vuông đó bằng: 1dm1dm,
32dm32dm, √2dm2dm hay 43dm43dm ?
Bài giải:
a) Gọi đường chéo của hình vuông có độ dài là aa.
Ta có: a2=32+32=18a2=32+32=18
Suy ra a=√18a=18
Vậy đường chéo của hình vuông đó bằng √18cm18cm.
b) Gọi cạnh của hình vuông là aa.
Ta có a2+a2=22⇒2a2=4⇒a2=2⇒a=√2a2+a2=22⇒2a2=4⇒a2=2⇒a=2
Vậy cạnh của hình vuông đó bằng √2dm2dm.


Câu 1:
Cho: ![]()
Tính giá trị P = x + y + xy
Câu 2:
Giải phương trình:
(a,b,c là hằng số và đôi một khác nhau)
Câu 3:
Xác định các số a, b biết: ![]()
Câu 4:
Chứng minh phương trình: 2x2 – 4y = 10 không có nghiệm nguyên.
Câu 5:
Cho tam giác ABC; AB = 3AC. Tính tỷ số đường cao xuất phát từ B và C
Câu 6:
Cho a, b, c thoả mãn: ![]()
Tính giá trị: ![]()
Câu 7:
Xác định a, b để f(x) = 6x4 – 7x3 + ax2 + 3x + 2
Chia hết cho y(x) = x2 – x + b
Câu 8:
Giải phương trình:
a, (x - 4)(x - 5)(x - 6)(x - 7) = 1680.
b, 4x2 + 4y – 4xy +5y2 + 1 = 0
Câu 9:
Tìm giá trị lớn nhất của phân số mà tử số là một số có 3 chữ số mà mẫu là tổng các chữ số của nó.
Câu 10:
Cho ABC cân tại A, trên AB lấy D, trên AC lấy E sao cho: AD = EC = DE = CB.
a, Nếu AB > 2BC. Tính góc A của ΔABC
b, Nếu AB < BC. Tính góc A của ΔHBC.
Câu 11:
Phân tích thành nhân tử:
a, a3 + b3 + c3 – 3abc
b, (x - y)3 +(y - z)3 + (z - x)3
Câu12:
a, Rút gọn A
b, Tìm A khi x = -1/2
c, Tìm x để 2A = 1
Câu 13:

a, Cho x + y + z = 3. Tìm giá trị nhỏ nhất của M = x2 + y2 + z2
b, Tìm giá trị lớn nhất của P = x/(x + 10)2
Câu 14:
a, Cho a, b, c > 0, CMR:
![]()
b, Cho x,y 0 CMR:
![]()
Câu 15:
Cho ∆ABC đều có độ dài cạnh là a, kéo dài BC một đoạn CM = a
a, Tính số đo các góc ∆ACM
b, CMR: AM ┴ AB
c, Kéo dài CA đoạn AN = a, kéo dài AB đoạn BP = a. CMR ∆MNP đều.
Giai các phương trình sau:
a) \(\frac{x^2-2x+1}{x^2-2x+2}+\frac{x^2-2x+2}{x^2-2x+3}=\frac{7}{6}\)
b) \(\frac{\left(x+1\right)^2}{x^2+2x+2}-\frac{x^2+2x}{\left(x+1\right)^2}=\frac{1}{90}\)
c) \(\frac{2x}{2x^2-5x+3}+\frac{13x}{2x^2+x+3}=6\)
d) \(\frac{x^2}{x^2+2x+2}+\frac{x^2}{x^2-2x+2}=\frac{5\left(x^2-5\right)}{x^2+4}+\frac{25}{4}\)
e) \(2\left(x+\frac{1}{x}\right)=\frac{x}{2}+x^2\)
g) \(\left(x-3\right)^4+\left(x-5\right)^4=16\)
h) \(\left(x-9\right)^4+\left(x-10\right)^4=\left(19-2x\right)^4\)
i) \(\left(6-x\right)^5+\left(x-4\right)^5=32\)
các bạn ơi hu hu hu