
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mk làm thế này ko bit có đúng ko?
\(a+b+c=0\Rightarrow\left(a+b+c\right)^2=0\Rightarrow a^2+b^2+c^2=-2\left(ab+bc+ac\right).\)
\(\Rightarrow ab+bc+ac=-5\)
\(\Rightarrow\left(ab+bc+ac\right)^2=25\Rightarrow a^2b^2+b^2c^2+c^2a^2+2ab^2c+2abc^2+2a^2bc=25.\)
\(\Rightarrow a^2b^2+b^2c^2+a^2c^2+2abc\left(a+b+c\right)=25.\)
\(\Rightarrow a^2b^2+b^2c^2+a^2c^2=25\)
Mặt khác:
\(a^2+b^2+c^2=10\Rightarrow\left(a^2+b^2+c^2\right)^2=100\)
\(\Rightarrow a^4+b^4+c^4+2\left(a^2b^2+b^2c^2+c^2a^2\right)=100\Rightarrow a^4+b^4+c^4+50=100\)
\(\Rightarrow a^4+b^4+c^4=50\).

Bài 1:
a: \(3x\left(x-2\right)=3x^2-6x\)
b: \(4x\left(x^2-3x+1\right)=4x^3-12x^2+4x\)
c: \(=3x^2-4x+6x-8=3x^2+2x-8\)

Kham khảo đề tự luận này nè bọn mình thi chúng đấy
Câu 1 (2,0 điểm) Thực hiện phép tính:
a) 2xy.3x2y3
b) x.(x2 - 2x + 5)
c) (3x2 - 6x) : 3x
d) (x2 – 2x + 1) : (x – 1)
Câu 2 (2,0 điểm). Phân tích các đa thức sau thành nhân tử:
a) 5x2y - 10xy2
b) 3(x + 3) – x2 + 9
c) x2 – y2 + xz - yz
Câu 3 (2,0 điểm). Cho biểu thức:
a) Với điều kiện nào của x thì giá trị của biểu thức A được xác định?
b) Rút gọn biểu thức A.
c) Tìm giá trị của biểu thức A tại x = 1.
Câu 4 (3,5 điểm). Cho tam giác MNP vuông tại M, đường cao MH. Gọi D, E lần lượt là chân các đường vuông góc hạ từ H xuống MN và MP.
a) Chứng minh tứ giác MDHE là hình chữ nhật.
b) Gọi A là trung điểm của HP. Chứng minh tam giác DEA vuông.
c) Tam giác MNP cần có thêm điều kiện gì để DE = 2EA.
Câu 5 (0,5 điểm). Cho a + b = 1. Tính giá trị của các biểu thức sau:
M = a3 + b3 + 3ab(a2 + b2) + 6a2b2(a + b).
Tham khảo nek :
Bài 1: (3 điểm) Giải phương trình và bất phương trình:
C) x – 2)2 + 2(x – 1) ≤ x2 + 4
Bài 2: (2 điểm) Một ô tô đi từ A đến B với vận tốc 60km/h và đi từ B về A với vận tốc 45km/h. Thời gian cả đi và về hết 7 giờ. Tính quãng đường AB.
Bài 3: (1 điểm)Chứng minh rằng nếu a + b = 1 thì a2 + b2 ≥ 1/2
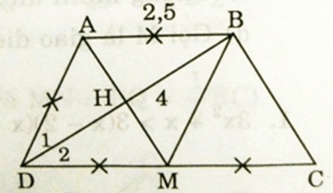
Bài 4: (4 điểm) Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
Đáp án và Hướng dẫn giải
Bài 1
a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2
(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)
Vậy tập nghiệm của pt là: S = {-1; 1}
b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0
Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x
⇔ x = -5 hoặc x = 5/3
Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}
c) x – 2)2 + 2(x – 1) ≤ x2 + 4
⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4
⇔ -2x ≤ 2
⇔ x ≥ -1
Tập nghiệm S = {x | x ≥ -1}
Bài 2
Gọi x (km) là quãng đường AB (x > 0)
Thời gian đi từ A đến B là: x/60 (giờ)
Thời gian đi từ B về A là: x/45 (giờ)
Theo đề ra, ta có phương trình:
⇔ 3x + 4x = 7.180 ⇔ 7x = 7.180 ⇔ x = 180 (nhận)
Trả lời: Quãng đường AB dài 180km.
Bài 3
Ta có: a + b = 1 ⇔ b = 1 – a
Thay vào bất đẳng thức a2 + b2 ≥ 1/2 , ta được:
a2 + (1 – a)2 ≥ 1/2 ⇔ a2 + 1 – 2a + a2 ≥ 1/2
⇔ 2a2 – 2a + 1 ≥ 1/2 ⇔ 4a2 – 4a + 2 ≥ 1
⇔ 4a2 – 4a + 1 ≥ 0 ⇔ (2a – 1)2 ≥ 0 (luôn đúng)
Vậy bất đẳng thức được chứng minh
Bài 4
a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
Xét tam giác vuông AHB, ta có :
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)

Mình mới lớp 5 thôi nhưng mình sẽ cho bạn 1 câu trả lời
Số 3
Xin lỗi bạn nhé mong bạn thông cảm
Đặt \(n+6=a^2;n+1=b^2\)Ta có:
\(a^2-b^2=\left(n+6\right)-\left(n+1\right)\)
\(\Leftrightarrow\left(a+b\right)\left(a-b\right)=5\)
Ta có bảng:
| a+b | 1 | 5 | -1 | -5 |
| a-b | 5 | 1 | -5 | -1 |
| a | 3 | 3 | -3 | -3 |
| b | 2 | -2 | -2 | 2 |
| a2=n+6 | 9 | 9 | 9 | 9 |
| b2=n+1 | 4 | 4 | 4 | 4 |
| n | 3 | 3 | 3 | 3 |
| Thỏa mãn | Thỏa mãn | Thỏa mãn | Thỏa mãn |
Vậy n=3


Bài 3:
a: Xét ΔADC có
\(\dfrac{AM}{MD}=\dfrac{AP}{PC}\)
Do đó: MP//DC
Xét ΔCAB có
\(\dfrac{CQ}{QB}=\dfrac{CP}{PA}\)
Do đó: PQ//AB
hay PQ//CD
Xét ΔBCD có
\(\dfrac{BQ}{QC}=\dfrac{BN}{ND}\)
Do đó: NQ//DC
Ta có: PQ//CD
NQ//DC
mà PQ và NQ có điểm chung là Q
nên Q,P,N thẳng hàng(1)
Ta có: PQ//CD
PM//CD
mà PQ và PM có điểm chung là P
nên M,P,Q thẳng hàng(2)
Từ (1) và (2) suy ra M,N,P,Q thẳng hàng
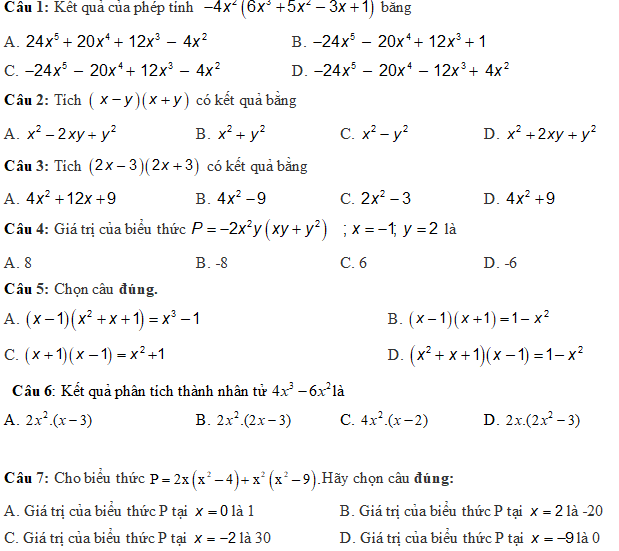

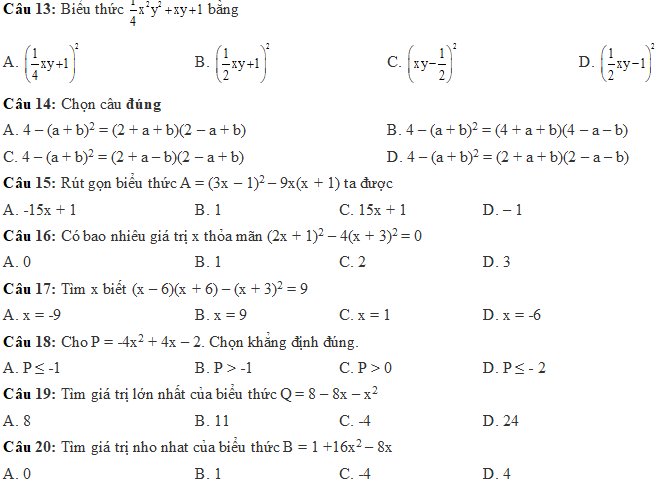



 các bạn làm cho mình đc ko ';-;
các bạn làm cho mình đc ko ';-;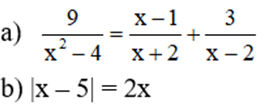
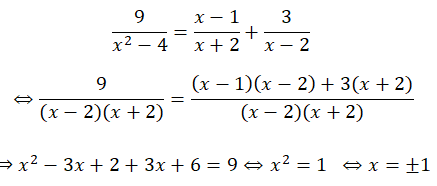
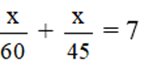
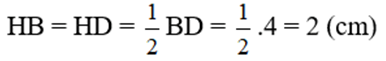
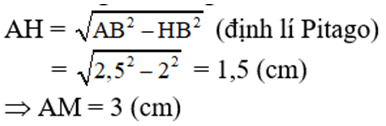
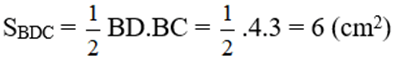

 giúp e vs ạ phần trắc nghiệm + bt ạ
giúp e vs ạ phần trắc nghiệm + bt ạ
\(33,x^2-6x+8=x^2-2x-4x+8=\left(x-2\right)\left(x-4\right)\\ 34,x^2-7x+10=x^2-2x-5x+10=\left(x-2\right)\left(x-5\right)\)