K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
6 tháng 7 2021
hình như ad có sự nhầm lẫn gì đó ở đây ạ :D
chỉ nêu về sự hiểu biết của cá nhân: ad bị nhầm về trình tự làm của bài toán này mất rồi
f(|x+m|) nguyên tắc là đối xứng rồi mới tịnh tiến cơ mà ad lại đi tịnh tiến trước
qua nguyên tắc trên ta cũng rút ra được quy tắc: số điểm cực trị của y=f(|x|) cũng bằng với số điểm cực trị y=f(|x+m|) cụ thể ở bài toán là bằng 3
AH
Akai Haruma
Giáo viên
6 tháng 7 2021
Lời giải:
Theo đồ thị thì $f(x)$ đạt cực trị tại $x=-2$ và $x=4$. Ta biết rằng dạng đồ thị hàm số $y=f(|x|)$ thì ta giữ nguyên phần đồ thị nằm bên phải trục tung, sau đó lấy đối xứng qua trục tung phần đồ thị bên phải.
Vậy ở bên phải trục tung ta đã có cực trị tại $x=4$ rồi thì lấy đối xứng qua trục tung ta có thêm 1 cực trị nữa. Thêm 1 cực trị tại $x=0$ (do tính đối xứng 2 bên tạo nên). Nên tổng cộng đồ thị $f(|x|)$ có 3 cực trị.
Tịnh tiến sang phải 3 đơn vị, ta có đồ thị hàm số $f(|x-3|)$ nên đồ thị $f(|x-3|)$ cũng có 3 cực trị tại $x=-1; x=3; x=7$
Đáp án C.
HN
10 tháng 10 2021
5) TCĐ: x=1 (loại C), điểm(-1;0) thuộc đồ thị (loại A, B)
Chọn D.
6, 7) TCN: y=1 (loại C), TCĐ: x=0 (loại B), điểm (1;0) thuộc đồ thị (loại A)
Chọn D.
8) TCĐ: x=1 (loại B), \(\exists\)x\(\in\)(-3;-2)|y=0 (loại A, B)
Chọn D.
9) TCN: y=2 (loại B, D), TCĐ: x=-1 (loại A)
Chọn C.
10) TCN: y=1 (loại A, B), TCĐ: x=1 (loại D)
Chọn C.
11) TCN: y=1 (loại A), TCĐ: x=1 (loại C), D=ad-bc < 0 (loại D)
Chọn B.
12) TCN: y=2 (loại A), TCĐ: x=-1(loại D), D=ad-bc > 0 (loại C)
Chọn B.
13) TCN: y=1 (loại A, B), TCĐ: x=2 (loại D)
Chọn C.
14) TCĐ: x=0,5 (loại B, C, D)
Chọn A.
15) TCN: y=a= -1< 0, x=0 \(\Rightarrow\) y=b= -2< 0. Vậy b<a<0.
Chọn C.
16) x=0 \(\Rightarrow\) y=\(-\dfrac{1}{d}\)> 0 \(\Rightarrow\) d<0, y=0 \(\Rightarrow\) x=\(\dfrac{1}{a}\)> 0 \(\Rightarrow\) a>0 (loại A, B, D)
Chọn C.
NL
1
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 6 2021
\(y'=\left(m+3\right)x^2-4x+m\)
Hàm nghịch biến trên R khi và chỉ khi \(y'\le0\) ; \(\forall x\in R\)
- Với \(m=-3\) ko thỏa mãn
- Với \(m\ne-3\) bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}m+3< 0\\\Delta'=4-m\left(m+3\right)\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< -3\\\left[{}\begin{matrix}m\ge1\\m\le-4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow m\le-4\)
UH
1
19 tháng 6 2016
txđ D=R
y'=-3x2+6x+3m
y' là tam thức bậc 2 nên y'=0 có tối đa 2 nghiệm
để hs nb/(0;\(+\infty\) ) thì y' \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) -3x2 +6x+3m \(\le\) 0 với mọi x \(\in\) (0;\(+\infty\) )
\(\Leftrightarrow\) m\(\le\) x2 -2x với mọi x \(\in\) (0; \(+\infty\) )
xét hs g(x)=x2 -2x
g'(X) =2x-2
g'(x)=0 \(\Leftrightarrow\) x=1
vậy m \(\le\) -1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 11 2021
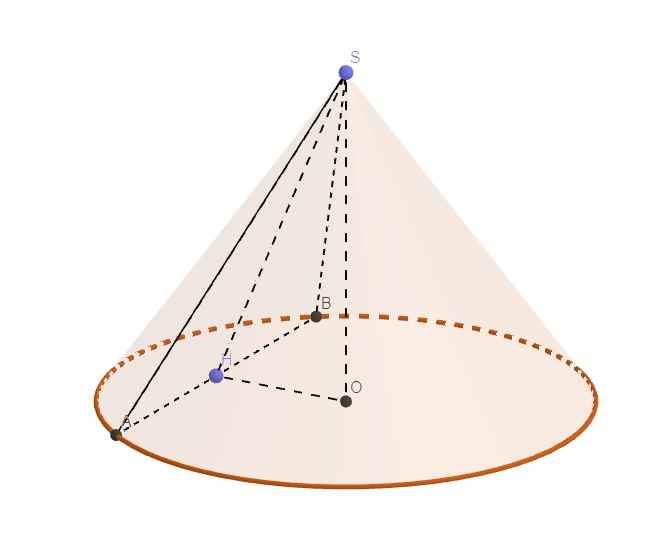
Đặt tên các điểm như hình vẽ, với H là trung điểm AB
\(\Rightarrow\widehat{SHO}=60^0\) (là góc giữa thiết diện và đáy nón)
Tam giác SAB đều \(\Rightarrow SH=\dfrac{AB\sqrt{3}}{2}=2\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow\left\{{}\begin{matrix}OH=SH.cos60^0=\sqrt{3}\\h=SO=SH.sin60^0=3\end{matrix}\right.\)
\(R=OA=\sqrt{AH^2+OH^2}=\sqrt{2^2+3}=\sqrt{7}\)
\(\Rightarrow V=\dfrac{1}{3}\pi R^2h=\dfrac{1}{3}\pi.7.3=7\pi\left(cm^3\right)\)
MA
0
20 tháng 4 2020
Hướng dẫn cách hack VIP OLM Vĩnh Viễn siêu dễ chỉ 10 phút là xong: youtube.com/watch?v=zYcnHqUcGZE&t
20 tháng 7 2016
Mình thấy có phân biệt gì giữa hàm đa thức và phân thức đâu bạn.
Theo định nghĩa thì hàm đạt cực trị tại y'=0; đồng biến khi y' > 0 và nghịch biến khi y' < 0.
Cách làm bài hàm bậc 3 ở trên là chưa chính xác.
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 5 2021
Phương trình mặt phẳng (P) qua A và vuông góc \(\overrightarrow{a}\) có dạng:
\(4\left(x-1\right)+2\left(y-1\right)-1\left(z+2\right)=0\)
\(\Leftrightarrow4x+2y-z-8=0\)
Gọi B là giao điểm (P) và \(\Delta\Rightarrow\) tọa độ B thỏa mãn:
\(4\left(2-t\right)+2\left(3+2t\right)-\left(1+3t\right)-8=0\) \(\Rightarrow t=\dfrac{5}{3}\) \(\Rightarrow B\left(\dfrac{1}{3};\dfrac{19}{3};6\right)\)
\(\Rightarrow\overrightarrow{AB}=\left(-\dfrac{2}{3};\dfrac{16}{3};8\right)=\dfrac{2}{3}\left(-1;8;12\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=1-t\\y=1+8t\\z=-2+12t\end{matrix}\right.\)
\(f\left(x\right)=\frac{x+m}{x+1}\)với \(x\in\left[0,1\right]\).
\(f'\left(x\right)=\frac{1-m}{\left(x+1\right)^2}\)
Với \(m=1\): \(f'\left(x\right)=0,\forall x\in\left[0,1\right]\)
\(f\left(x\right)=1\)suy ra \(max_{\left[0,1\right]}\left|f\left(x\right)\right|+min_{\left[0,1\right]}\left|f\left(x\right)\right|=1+1=2\)thỏa mãn.
Với \(m\ne1\): \(f'\left(x\right)\)đơn điệu với \(x\in\left[0,1\right]\).
Ta có: \(f\left(0\right)=m,f\left(1\right)=\frac{m+1}{2}\).
Với \(f\left(0\right)f\left(1\right)\ge0\Leftrightarrow\orbr{\begin{cases}m\ge0\\m\le-1\end{cases}}\)ta có:
\(max_{\left[0,1\right]}\left|f\left(x\right)\right|+min_{\left[0,1\right]}\left|f\left(x\right)\right|=\left|m\right|+\left|\frac{m+1}{2}\right|\)
\(=\left|\frac{3m+1}{2}\right|=2\Leftrightarrow\orbr{\begin{cases}m=1\left(l\right)\\m=-\frac{5}{3}\left(tm\right)\end{cases}}\)
Với \(f\left(0\right)f\left(1\right)< 0\Leftrightarrow-1< m< 0\).
Khi đó \(min_{\left[0,1\right]}\left|f\left(x\right)\right|=0,max_{\left[0,1\right]}\left|f\left(x\right)\right|=max\left\{\left|f\left(0\right)\right|,\left|f\left(1\right)\right|\right\}\).
\(max_{\left[0,1\right]}\left|f\left(x\right)\right|+min_{\left[0,1\right]}\left|f\left(x\right)\right|=max\left\{\left|f\left(0\right)\right|,\left|f\left(1\right)\right|\right\}\)
\(=max\left\{\left|m\right|,\left|\frac{m+1}{2}\right|\right\}=2\)
\(\Rightarrow\orbr{\begin{cases}\left|m\right|=2\\\left|\frac{m+1}{2}\right|=2\end{cases}}\)
Giải ra các giá trị của \(m\)ta thấy đều không thỏa mãn.
Vậy \(m\in\left\{1,-\frac{5}{3}\right\}\).
Chọn B.