K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TM
18 tháng 1 2022
a. \(D=\left(\dfrac{x^2-3x}{x^2-9}-1\right):\left(\dfrac{9-x^2}{x^2+x-6}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right)\)
\(=\left[\dfrac{x\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-1\right]:\left[\dfrac{\left(3-x\right)\left(3+x\right)}{x^2-2x+3x-6}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right]\)
\(=\left(\dfrac{x}{x+3}-1\right):\left[\dfrac{\left(3-x\right)\left(3+x\right)}{x\left(x-2\right)+3\left(x-2\right)}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right]\)
\(=\left(\dfrac{x}{x+3}-\dfrac{x+3}{x+3}\right):\left[\dfrac{\left(3-x\right)\left(3+x\right)}{\left(x-2\right)\left(x+3\right)}-\dfrac{x-3}{2-x}-\dfrac{x-2}{x+3}\right]\)
\(=\dfrac{3}{x+3}:\left(\dfrac{3-x}{x-2}-\dfrac{3-x}{x-2}-\dfrac{x-2}{x+3}\right)\)
\(=\dfrac{3}{x+3}:\dfrac{x-2}{x+3}\)
\(=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-2\right)}=\dfrac{3}{x-2}\)
4 tháng 10 2021
Bài 3:
b: Xét ΔABC có
I là trung điểm của BC
IK//AC
Do đó: K là trung điểm của AB
Xét ΔABC có
I là trung điểm của BC
IH//AB
Do đó: H là trung điểm của AC
Xét ΔABC có
K là trung điểm của AB
H là trung điểm của AC
Do đó: HK là đường trung bình của ΔABC
Suy ra: HK//BC
10 tháng 1 2022
a: ĐKXĐ: \(x\notin\left\{2;-2;0\right\}\)
b: \(P=\left(\dfrac{-\left(x+2\right)}{x-2}+\dfrac{4x^2}{\left(x-2\right)\left(x+2\right)}+\dfrac{x-2}{x+2}\right)\cdot\dfrac{-x^2\left(x-2\right)}{x\left(x-3\right)}\)
\(=\dfrac{-x^2-4x-4+4x^2+x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{-x\left(x-2\right)}{x-3}\)
\(=\dfrac{4x^2-8x}{x+2}\cdot\dfrac{-x}{x-3}=\dfrac{-4x^2\left(x-2\right)}{\left(x+2\right)\left(x-3\right)}\)
KC
2
17 tháng 4 2022
\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)
19 tháng 12 2021
a: Xét tứ giác DEBF có
BE//DF
BE=DF
Do đó: DEBF là hình bình hành
Suy ra: DE//BF
22 tháng 11 2021
a) Xét tứ giác AHCK có:
I là trung điểm của AC và HK
=> AHCK là hình bình hành
Mà \(\widehat{AHC}=90^0\)(AH là đường cao)
=> AHCK là hình chữ nhật
b) Ta có: K//HC và AK=HC(AHCK là hình bình hành)
Mà H∈BC và BH=HC
=> AK//BH và AK=BH
=> AKHB là hình bình hành
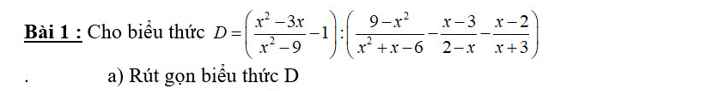
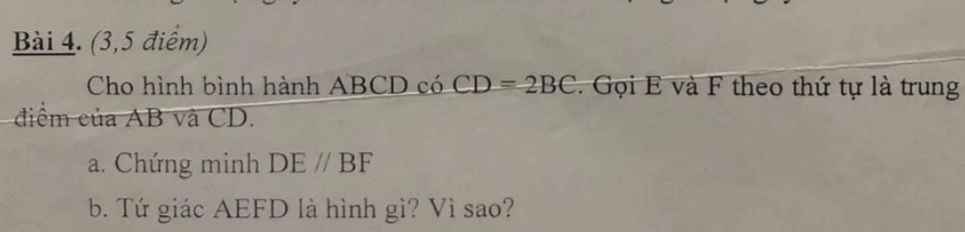
Gọi vận tốc xe ô tô thứ nhất, thứ 2 lần lượt là a ; b ( a ; b )
Theo bài ra ta có
\(\dfrac{60}{x-10}-\dfrac{60}{x}=\dfrac{3}{10}\Rightarrow x=50\)
Vậy ...