
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,=\left(\sqrt{a}-1\right)\left(a+\sqrt{a}+1\right)\\ b,=\left(\sqrt{x}-\sqrt{y}\right)\left(\sqrt{x}+\sqrt{y}\right)-2\left(\sqrt{x}+\sqrt{y}\right)\\ =\left(\sqrt{x}+\sqrt{y}\right)\left(\sqrt{x}-\sqrt{y}-2\right)\\ c,=x\left(\sqrt{x}-1\right)-\left(\sqrt{x}-1\right)=\left(\sqrt{x}-1\right)^2\left(\sqrt{x}+1\right)\)
\(a,=\dfrac{\left(9-4\sqrt{5}\right)\left(5+2\sqrt{5}\right)}{4}+\dfrac{2\sqrt{5}}{5}\\ =\dfrac{5-2\sqrt{5}}{4}+\dfrac{2\sqrt{5}}{5}\\ =\dfrac{25-10\sqrt{5}+8\sqrt{5}}{20}=\dfrac{25-2\sqrt{5}}{20}\\ b,=\dfrac{\sqrt{x}+2-4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{1}{\sqrt{x}+2}\\ c,=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2}-\dfrac{2}{\sqrt{x}-1}\\ =\dfrac{\sqrt{x}+1-2}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}-1}=1\\ d,=\dfrac{1}{\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}+\dfrac{x+1}{1-x}\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}-1-x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{2\sqrt{x}-x-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{-\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\)

a: Xét (O) có
ΔAIB nội tiếp
AB là đường kính
=>ΔAIB vuông tại I
Xét ΔBAE có
BI vừa là đường cao, vừa là phân giác
nên ΔBAE cân tại B
b: Xét (O) có
ΔACB nội tiếp
AB là đường kính
=>ΔBCA vuông tại C
Xét ΔEAB co
BI.AC là các đường cao
BI cắt AC tại K
=>K là trực tâm
=>EK vuông góc với AB

Bài 2:
a: Gọi (d): y=ax+b là phương trìnhđường thẳng cần tìm
Vì (d) đi qua A(1;-2) và B(2;1) nên ta có hệ:
a+b=-2 và 2a+b=1
=>a=3 và b=-5
b: Gọi (d): y=ax+b là phương trìnhđường thẳng cần tìm
Vì (d) có hệ số góc là 2 nên a=2
=>y=2x+b
Thay x=1 và y=5 vào (d), ta được:
b+2=5
=>b=3
c: Gọi (d): y=ax+b là phương trìnhđường thẳng cần tìm
Vì (d)//y=4x+3
nên a=4
=>y=4x+b
Thay x=-1 và y=8 vào (d), ta được:
b-4=8
=>b=12
d: Gọi (d): y=ax+b là phương trìnhđường thẳng cần tìm
Vì (d)//y=-x+5
nên a=-1
=>y=-x+b
Thay x=2 và y=0 vào (d), ta được:
b-2=0
=>b=2

\(P=\left(x^2+2x\right)\left(y^2-4y\right)+5\left(x^2+2x\right)+4\left(y^2-4y\right)+2021\)
\(=\left[\left(x+1\right)^2-1\right]\left[\left(y-2\right)^2-4\right]+5\left(x+1\right)^2+4\left(y-2\right)^2+2000\)
\(=\left(x+1\right)^2\left(y-2\right)^2+\left(x+1\right)^2+3\left(y-2\right)^2+2024\ge2024\)
\(P_{min}=2024\) khi \(\left(x;y\right)=\left(-1;2\right)\)

3: \(=7-4\sqrt{3}+7+4\sqrt{3}=14\)
4: \(=\left(\dfrac{\sqrt{5}+\sqrt{2}-\sqrt{5}+\sqrt{2}+3}{3}\right)\cdot\dfrac{1}{3+2\sqrt{2}}=\dfrac{1}{3}\)

Bài 1:
a: Thay x=4 vào A, ta được:
\(A=\dfrac{3}{2-1}=3\)

Bạn nên tách lẻ các bài ra post riêng. Đăng thế này chiếm diện tích, khó quan sát => mọi người dễ bỏ qua bài của bạn.

\(x=\sqrt{9+4\sqrt{5}}-\sqrt{9-4\sqrt{5}}\)
\(=\sqrt{\left(\sqrt{5}+2\right)^2}-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=\left|\sqrt{5}+2\right|-\left|\sqrt{5}-2\right|\)
\(=\sqrt{5}+2-\sqrt{5}+2=4\)
\(y=\sqrt{3+2\sqrt{5}}-\sqrt{3-2\sqrt{5}}\)
Xem lại đề, \(\sqrt{3-2\sqrt{5}}\) không xác định.

a)
\(\sqrt{9+4\sqrt{5}}\cdot\sqrt{6-2\sqrt{5}}\\ =\sqrt{4+4\sqrt{5}+5}\cdot\sqrt{1-2\sqrt{5}+5}\\ =\sqrt{\left(2+\sqrt{5}\right)^2}\cdot\sqrt{\left(1-\sqrt{5}\right)^2}\\ =\left(2+\sqrt{5}\right)\left(1-\sqrt{5}\right)\)
b)
\(\sqrt{3+2\sqrt{2}}-\sqrt{6-4\sqrt{2}}\\ =\sqrt{2+2\sqrt{2}+1}-\sqrt{4-4\sqrt{2}+2}\\ =\sqrt{\left(\sqrt{2}+1\right)^2}-\sqrt{\left(2-\sqrt{2}\right)^2}\\ =\sqrt{2}+1-2+\sqrt{2}=2\sqrt{2}-1\)
 các bạn giúp m c này với!
các bạn giúp m c này với!



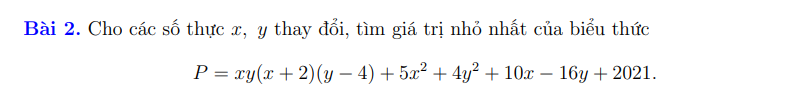
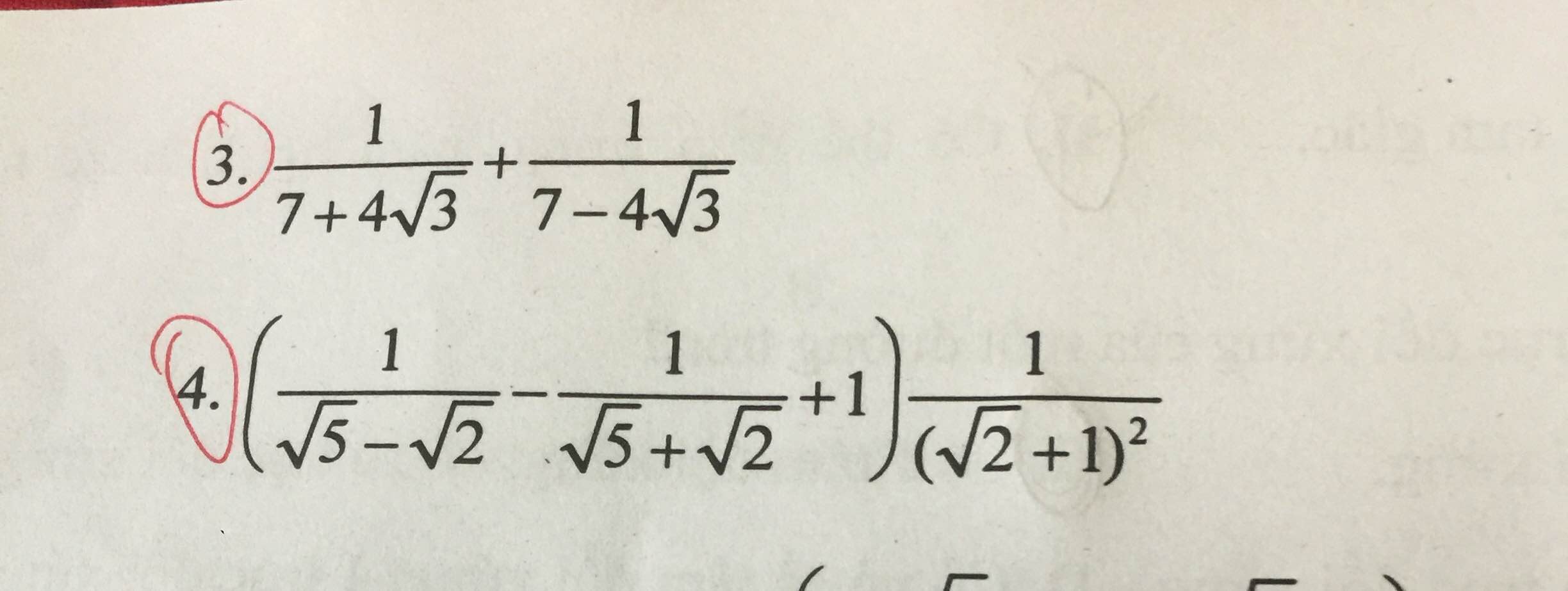

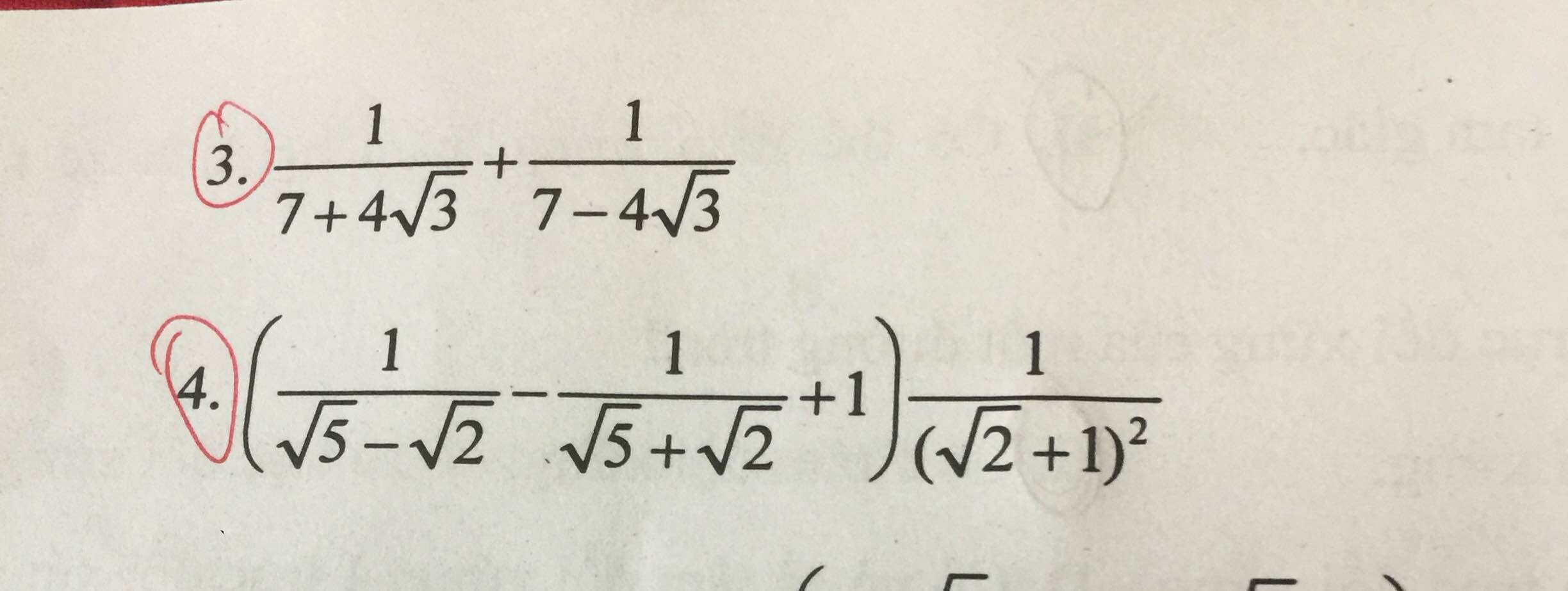




a/ Ta có
\(OM\perp xy\) (Tiếp tuyến vuông góc với bán kính tại tiếp điểm)
\(AC\perp xy;BD\perp xy\)
=> AC//OM//BD \(\Rightarrow\frac{MC}{MD}=\frac{OA}{OB}=1\Rightarrow MC=MD\)
b/
Ta có
AC//OM//BD
MC=MD; OA=OB
=> OM là đường trung bình của hình thang ACDB \(\Rightarrow OM=\frac{AC+BD}{2}\Rightarrow AC+BD=2.OM=2R\) không đổi
c/ Từ M dựng đường thảng vuông góc với AB cắt AB tại H
Xét tg MAB có \(\widehat{AMB}=90^o\) (góc nội tiếp chắn nửa đường tròn) => tg MAB vuông tại M
\(\Rightarrow\widehat{ABM}+\widehat{MAB}=90^o\)
Xét tg vuông AHM có \(\widehat{AMH}+\widehat{MAB}=90^o\)
\(\Rightarrow\widehat{AMH}=\widehat{ABM}\) (1)
Ta có
\(sd\widehat{ABM}=\frac{1}{2}\)sd cung AM (góc nội tiếp đường tròn)
\(sd\widehat{AMC}=\frac{1}{2}\)sd cung AM (góc giữa tiếp tuyến và dây cung)
\(\Rightarrow\widehat{AMC}=\widehat{ABM}\) (2)
Xét tg vuông ACM và tg vuông AHM có
AM chung
Từ (1) VÀ (2) \(\Rightarrow\widehat{AMC}=\widehat{AMH}\)
\(\Rightarrow\Delta ACM=\Delta AHM\) (2 tg vuông có cạnh huyền và 1 góc nhọn tương ứng bằng nhau thì bằng nhau)
\(\Rightarrow MC=MH\Rightarrow MC=MH=MD\)
=> C; H; D cùng nằm trên đường tròn tâm M đường kính CD
Mà \(AB\perp MH\)
=> AB là tiếp tuyến của đường tròn đường kính CD (Đường thẳng vuông góc với bán kính tại 1 điểm thuộc đường tròn là tiếp tuyến)