Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi E là giao điểm của AC và BD.
∆ECD có ∠C1 = ∠D1 (do ∠ACD = ∠BDC) nên là tam giác cân.
Suy ra EC = ED (1)
Tương tự ∆EAB cân tại A suy ra: EA = EB (2)
Từ (1) và (2) ta có: EA + EC = EB + ED ⇒ AC = BD
Hình thang ABCD có hai đường chéo bằng nhau nên là hình thang cân.4

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bằng nhau nên là hình bình hành theo dấu hiệu nhận biết 5
b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa)
c) Sai.
Ví dụ tứ giác ABCD ở dưới có AB = CD nhưng không phải hình bình hành.
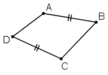
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

Gọi số câu đúng là x; số câu sai là y.
Ta có tổng số câu là 10.
Ta có hệ phương trình:
x + y = 10
10x - 5y = 85
Giải hệ ra được: x = 9 và y = 1
Vậy bạn đó trả lời đúng 8 câu.
Giả sử thì sinh đó trả lời đúng hết thì sẽ có số điểm là: \(10.10=100\)(điểm)
Vì bạn đó được 85 điểm nên số điểm bị thừa là: \(100-85=15\)(điểm)
Số câu trả lời đúng là: \(10 - 15:(5+10)= 9\)(câu)
Vậy bạn đó đã trả lời đúng \(9\) câu

a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bàng nhau nên là hình bình hành theo dấu hiệu nhận biết 5.
b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa).
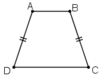
c) Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành.
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.
Bài giải:
a) Đúng, vì hình thang có hai đáy song song lại có thêm hai cạnh đáy bàng nhau nên là hình bình hành theo dấu hiệu nhận biết 5.
b) Đúng, vì khi đó ta được tứ giác có các cạnh đối song song là hình bình hành (định nghĩa).
c) Sai, vì hình thang cân có hai cạnh đối (hai cạnh bên) bằng nhau nhưng nó không phải là hình bình hành.
d) Sai, vì hình thang cân có hai cạnh bên bằng nhau nhưng nó không phải là hình bình hành.

\(AH^2=BH.CH=18.32=576\Rightarrow AH=24\left(cm\right)\)
\(AB^2=AH^2+BH^2=576+324=900\) (Δ ABH vuông tại H)
\(\Rightarrow AB=30\left(cm\right)\)
\(AC^2=AH^2+CH^2=576+1024=1600\) (Δ ACH vuông tại H)
\(\Rightarrow AC=40\left(cm\right)\)
Xét tam giác AHB vuông tại H có:
AH2+HB2=AB2(định lý pythagore) (1)
Xét tam giác AHC vuông tại H có:
HA2+HC2=AC2 (định lý pythagore) (2)
Từ (1) và (2) ta cộng lại vế theo vế, có:
2AH2+BH2+CH2=AB2+AC2
<=>2AH2+BH2+CH2=BC2
<=> 2AH2+182+322=(18+32)2
<=>2AH2+1348=2500
<=>2AH2=2500-1348
<=>2AH2=1152
<=>AH2=1152:2
<=>AH2=576
<=>AH=\(\sqrt{576}\)
<=>AH=24(cm)
-Ta thay AH=24cm vào (1) ta có:
HB2+AH2=AB2
<=>182+242=AB2
<=>900=AB2
<=>\(AB=\sqrt{900}=30\)(cm)
-Ta thay AH=24cm vào (2) ta có:
HC2+HA2=AC2
<=>322+242=AC2
<=>1600=AC2
\(\Leftrightarrow AC=\sqrt{1600}=40\left(cm\right)\)
Vậy AB=30cm; AC=40cm

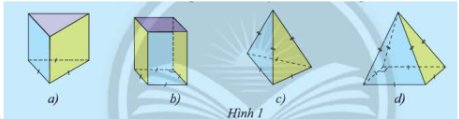
a) Các mặt bên của mỗi hình a, b là các hình chữ nhật
Các mặt bên của mỗi hình c, d là hình tam giác
b) Hình c có cách cạnh bên bằng nhau và đáy là tam giác đều
c) Hình d có các cạnh bên bằng nhau và đáy là hình vuông
a:
1a,1b: Hình chữ nhật
1c,1d: Hình tam giác
b:
Cả bốn hình đều có các cạnh bên bằng nhau
1c,1a là hai hình là các đáy là tam giác đều
c: Hình 1b và hình 1d có đáy là hình vuông
Trong hình thang vuông có cạnh nào bằng nhau sao?
Hình thang có hai cạnh đáy bằng nhau là hình bình hành