Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Hình minh họa)
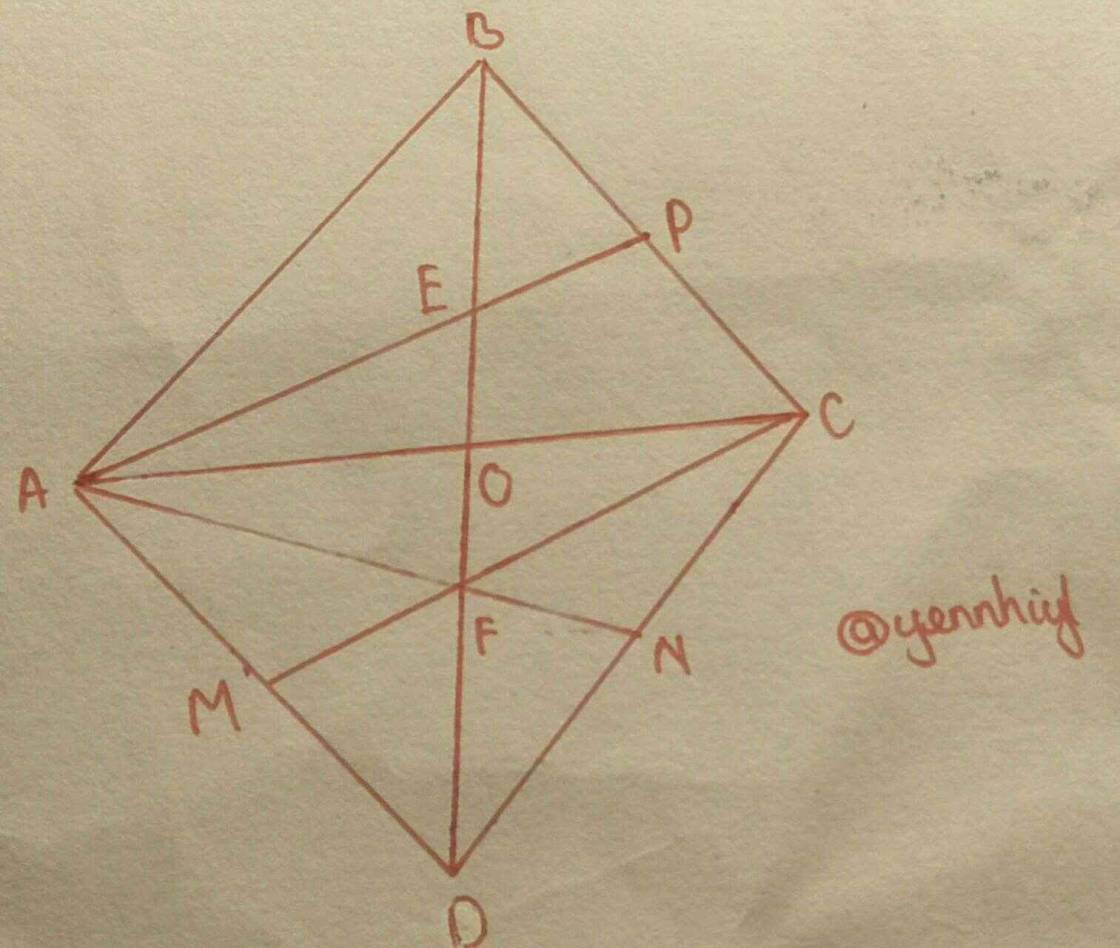
a)
Gọi O là giao điểm của AC và BD
Xét \(\Delta ABD\) và \(\Delta CDB\):
BD chung
\(\widehat{ABD}=\widehat{CDB}\)
\(\widehat{ADB}=\widehat{CBD}\)
\(\Rightarrow\Delta ABD=\Delta CBD\left(g.c.g\right)\)
\(\Rightarrow AB=CD\)
Xét \(\Delta AOB\) và \(\Delta COD\):
AB = CD
\(\widehat{OBA}=\widehat{ODC}\)
\(\widehat{OAB}=\widehat{OCD}\)
\(\Rightarrow\Delta AOB=\Delta COD\left(g.c.g\right)\)
\(\Rightarrow OA=OC;OB=OD\)
\(\Rightarrow O\) là trung điểm AC và BD
Xét \(\Delta ACD\):
MC và DO là hai đường trung tuyến của tam giác và giao nhau ở F
\(\Rightarrow F\) là trọng tâm \(\Delta ADC\)
Mà AN là đường trung tuyến \(\Delta ADC\)
\(\Rightarrow A,F,N\) thẳng hàng
b)
Vì P là trọng tâm \(\Delta ADC\)
\(\Rightarrow DF=\dfrac{2}{3}DO;OF=\dfrac{1}{3}DO\)
Vì O là giao điểm của hai đường trung tuyến BO và AP của \(\Delta ABC\)
\(\Rightarrow O\) là trọng tâm \(\Delta ABC\)
\(\Rightarrow BE=\dfrac{2}{3}BO;EO=\dfrac{1}{3}BO\)
Mà O là trung điểm BD
\(\Rightarrow BO=DO\)
\(\Rightarrow BE=DF=\dfrac{2}{3}BO=\dfrac{2}{3}DO\)
\(\Rightarrow FO=EO=\dfrac{1}{3}BO=\dfrac{1}{3}DO\Rightarrow EO+FO=FE=\dfrac{2}{3}BO=\dfrac{2}{3}DO\)
\(\Rightarrow BE=FE=FD\).

Xét ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
Do đó: ΔABD=ΔACD

a) Xét ΔAMB và ΔCMD có:
AM=MC (gt)
\(\widehat{AMB}=\widehat{CMD}\) (đối đỉnh)
BM=MD (gt)
=> ΔAMB=ΔCMD (c.g.c)
b) Xét ΔAKM và ΔCHM có:
AM=MC (gt)
\(\widehat{AMK}=\widehat{CMH}\) (đối đỉnh)
=> ΔAKM=ΔCHM (cạnh huyền-góc nhọn)
=> AK=CH (hai cạnh tương ứng)
c) Ta có: \(\widehat{AMK}=\widehat{DMC}\) (đối đỉnh)
Mà: \(\widehat{\text{AMF}}+\widehat{FMD}+\widehat{DMC}=180^o\)
=> \(\widehat{FMD}+\widehat{DMC}+\widehat{CME}=\widehat{FME}=180^o\)
Vậy ba điểm F,M,E thẳng hàng