K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
B
2
N
10 tháng 11 2021
Đổi 4 thành 2 mũ 2
Thử xem cs đúng ko . Vì mik chữ thầy toán giả thầy toán hết r
TN
10 tháng 11 2021
Dễ:đổi 4=22
B=22+23+24+...+220
ta có:B=2B-B=(23+24+25+...+221)-(22+23+24+...+220)
= 221-22
Nói trước: đây là mình rút gọn chứ viết mà theo cơ số 2 thì khó quá
16 tháng 10 2021
\(A=2+2^2+...+2^{20}\\ 2A=2^2+2^3+...+2^{21}\\ A=2^{21}-2\)
TH
3
H9
HT.Phong (9A5)
CTVHS
14 tháng 10 2023
\(A=2+2^2+...+2^{20}\)
\(2A=2^2+2^3+...+2^{21}\)
\(2A-A=2^2+2^3+...+2^{21}-2-2^2-...-2^{20}\)
\(A=2^{21}-2\)
___________
\(B=5+5^2+...+5^{50}\)
\(5B=5^2+5^3+...+5^{51}\)
\(5B-B=5^2+5^3+...+5^{51}-5-5^2-...-5^{50}\)
\(4B=5^{51}-5\)
\(B=\dfrac{5^{51}-5}{4}\)
___________
\(C=1+3+3^2+...+3^{100}\)
\(3C=3+3^2+...+3^{101}\)
\(3C-C=3+3^2+...+3^{101}-1-3-3^2-...-3^{100}\)
\(2C=3^{101}-1\)
\(C=\dfrac{3^{101}-1}{2}\)
19 tháng 2 2021
Ta có: 2 + 22 + 23 + ... + 220
= (2 + 22 + 23 + 24) + (25 + 26 + 27 + 28) + ... + (217 + 218 + 219 + 220)
= (2 + 22 + 23 + 24) + 24(2 + 22 + 23 + 24) + 28(2 + 22 + 23 + 24) + 216(2 + 22 + 23 + 24)
= (1 + 24 + 28 + 216)(2 + 22 + 23 + 24)
= 30(2 + 22 + 23 + 24)
Vì 30 có tận cùng là 0 nên 30(2 + 22 + 23 + 24) có tận cùng là 0
hay 2 + 22 + 23 + ... + 220 có tận cùng là 0
Chúc bn học tốt!
KV
22 tháng 10 2023
a) P = 1 + 3 + 3² + ... + 3¹⁰¹
= (1 + 3 + 3²) + (3³ + 3⁴ + 3⁵) + ... + (3⁹⁹ + 3¹⁰⁰ + 3¹⁰¹)
= 13 + 3³.(1 + 3 + 3²) + ... + 3⁹⁹.(1 + 3 + 3²)
= 13 + 3³.13 + ... + 3⁹⁹.13
= 13.(1 + 3³ + ... + 3⁹⁹) ⋮ 13
Vậy P ⋮ 13
b) B = 1 + 2² + 2⁴ + ... + 2²⁰²⁰
= (1 + 2² + 2⁴) + (2⁶ + 2⁸ + 2¹⁰) + ... + (2²⁰¹⁶ + 2²⁰¹⁸ + 2²⁰²⁰)
= 21 + 2⁶.(1 + 2² + 2⁴) + ... + 2²⁰¹⁶.(1 + 2² + 2⁴)
= 21 + 2⁶.21 + ... + 2²⁰¹⁶.21
= 21.(1 + 2⁶ + ... + 2²⁰¹⁶) ⋮ 21
Vậy B ⋮ 21
c) A = 2 + 2² + 2³ + ... + 2²⁰
= (2 + 2² + 2³ + 2⁴) + (2⁵ + 2⁶ + 2⁷ + 2⁸) + ... + (2¹⁷ + 2¹⁸ + 2¹⁹ + 2²⁰)
= 30 + 2⁴.(2 + 2² + 2³ + 2⁴) + ... + 2¹⁶.(2 + 2² + 2³ + 2⁴)
= 30 + 2⁴.30 + ... + 2¹⁶.30
= 30.(1 + 2⁴ + ... + 2¹⁶)
= 5.6.(1 + 2⁴ + ... + 2¹⁶) ⋮ 5
Vậy A ⋮ 5
d) A = 1 + 4 + 4² + ... + 4⁹⁸
= (1 + 4 + 4²) + (4³ + 4⁴ + 4⁵) + ... + (4⁹⁷ + 4⁹⁸ + 4⁹⁹)
= 21 + 4³.(1 + 4 + 4²) + ... + 4⁹⁷.(1 + 4 + 4²)
= 21 + 4³.21 + ... + 4⁹⁷.21
= 21.(1 + 4³ + ... + 4⁹⁷) ⋮ 21
Vậy A ⋮ 21
e) A = 11⁹ + 11⁸ + 11⁷ + ... + 11 + 1
= (11⁹ + 11⁸ + 11⁷ + 11⁶ + 11⁵) + (11⁴ + 11³ + 11² + 11 + 1)
= 11⁵.(11⁴ + 11³ + 11² + 11 + 1) + 16105
= 11⁵.16105 + 16105
= 16105.(11⁵ + 1)
= 5.3221.(11⁵ + 1) ⋮ 5
Vậy A ⋮ 5
NT
2
AH
Akai Haruma
Giáo viên
23 tháng 10 2023
Lời giải:
$A=(2+2^2)+(2^3+2^4)+....+(2^{19}+2^{20})$
$=2(1+2)+2^3(1+2)+....+2^{19}(1+2)$
$=(2+2^3+...+2^{19})(1+2)=(2+2^3+...+2^{19}).3\vdots 3(1)$
---------------------
Lại có:
$A=(2+2^2+2^3+2^4)+(2^5+2^6+2^7+2^8)+...+(2^{17}+2^{18}+2^{19}+2^{20})$
$=2(1+2+2^2+2^3)+2^5(1+2+2^2+2^3)+....+2^{17}(1+2+2^2+2^3)$
$=(1+2+2^2+2^3)(2+2^5+...+2^{17})$
$=15(2+2^5+...+2^{17})\vdots 15(2)$
Từ $(1); (2)$ ta có đpcm.
PG
23 tháng 10 2023
Ta có:
A=2+22+23+...+220
A=(2+22)+(23+24)...+(219+220)
A=2.(1+2)+23.(1+2)...+219.(1+2)
A=2.3+23.3...+219.3
A=3.(2+23+...+219)
vậy a chia hết cho 3 vì a=3k với k là số tự nhiên
Ta có:
A=2+22+23+...+220
A=(2+22+23+24)+(25+26+27+28)+...+(217+218+219+220)
A=2.(1+2+22+23)+25.(1+2+22+23)+...+217.(1+2+22+23)
A=2.(1+2+4+8)+25.(1+2+4+8)+...+217.(1+2+4+8)
A=2.15+25.15+...+217.15
A=(15.2.+25.+...+217)
vậy a chia hết cho 15 vì a=15k với k là số tự nhiên
CM
7 tháng 7 2019
a) A chia hết cho 2 vì tất cả các số hạng của tổng đều chia hết cho 2.
b) Ta tách ghép các số hạng của A thành các nhóm sao cho mỗi nhóm xuất hiện thừa số chia hết cho 3. Khi đó:
10 tháng 10 2021
4₁ A= 2 +2²³ +2 ² + + 220
a₁ A = 2₁ [1 + 2 +2²¹ +. +2¹2):2 Vay A chia hết choi
b₁ A = 2 + 2² +2²+ + 220 (2 +2²) + (2 ² + 2 9) + . + (219+220)
= 2₁ (1 + 2) + 2² (2+1). .. +2 19 (2+1) + = 2₁3 + 2³.3 + ..+ 219.3.
= (2+2 ³+ + 219) 3:3 Vậy A chia hết cho 3 A = 2 + 2 ² + 2³ + 2ª +. 20 + 2.9+ +2
2+2 ³ + 2² +2²4 + + 218 + 720 +2²³ +2²+ +218 +220 2. (2 +2²) + 2² (1+2²) +.. + 218 ( 1 +2²) = 2 5 +2²5 + + 218 5. 12 +2° + 2 ... +218 ) 5 : 5.
vậy A chia hết cho 5
GB
1
13 tháng 11 2023
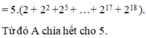
Sửa đề: \(A=2+2^2+2^3+2^4+...+2^{19}+2^{20}\)
=>\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{19}+2^{20}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^{19}\left(1+2\right)\)
\(=3\left(2+2^3+...+2^{19}\right)⋮3\)
TM
1
S
9 tháng 2 2021
A=2+22+23+...+220A=2+22+23+...+220
2A=22+23+24+...+2212A=22+23+24+...+221
2A−A=(22+23+24+...+221)−(2+22+23+...+220)2A−A=(22+23+24+...+221)−(2+22+23+...+220)
A=221−2=24.5+1−2=(24)5.2−2=165.2−2A=221−2=24.5+1−2=(24)5.2−2=165.2−2
A=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯.......6.2−2=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯........2−2=¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯...........0A=.......6¯.2−2=........2¯−2=...........0¯
Vậy chữ số tận cùng cả A là 0
\(C=4+2^2+2^3+...+2^{20}\)
\(\Rightarrow C=2^2+2^2+2^3+...+2^{20}\)
\(\Rightarrow2C=2\left(2^2+2^2+2^3+...+2^{20}\right)\)
\(\Rightarrow2C=2^3+2^3+2^4+...+2^{21}\)
\(\Rightarrow2C-C=2^{21}+2^3-2^2-2^2\)
\(\Rightarrow C=2^{21}+8-4-4\)
\(\Rightarrow C=2^{21}-0\)
\(\Rightarrow C=2^{21}\)