c và d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 2 2022
a: \(=\left(2+\dfrac{4}{9}+4+\dfrac{5}{9}\right)+\left(-4-\dfrac{13}{21}-2-\dfrac{8}{21}\right)\)
=7-7
=0
b: \(=\dfrac{5}{23}\left(\dfrac{7}{13}+\dfrac{6}{13}\right)+\dfrac{18}{23}=\dfrac{5}{23}+\dfrac{18}{23}=1\)
c: \(=\dfrac{3}{7}\left(\dfrac{12}{19}-\dfrac{4}{19}\right)+\dfrac{4}{7}\cdot\dfrac{8}{19}\)
\(=\dfrac{3}{7}\cdot\dfrac{8}{19}+\dfrac{4}{7}\cdot\dfrac{8}{19}=\dfrac{8}{19}\)
d: \(=\dfrac{2}{5}+\dfrac{3}{5}:\dfrac{9-10}{15}-\dfrac{7}{2}\)
\(=\dfrac{-31}{10}+\dfrac{3}{5}\cdot\dfrac{-15}{1}=\dfrac{-31}{10}-9=\dfrac{-121}{10}\)
26 tháng 7 2023
a: x^3+8=(x+2)(x^2-2x+4)
b: =(3x+1)(9x^2-3x+1)
c: =(x+3)(x^2-3x+9)
d: =(4x-3y)(16x^2+24xy+9y^2)
MP
26 tháng 7 2023
\(a.x^3+8=\left(x+2\right)\left(x^2-2x+4\right)\)
\(b.27x^3+1=\left(3x+1\right)\left(9x-3x+1\right)\)
\(c.x^3+27=\left(x+3\right)\left(x^2-3x+9\right)\)
\(d.64x^3-27y^3=\left(4x-3y\right)\left(16x^2+12xy+9y^2\right)\)
24 tháng 12 2023
Sửa đề: cắt DC tại M
a: Xét tứ giác ABMD có
AB//MD
AD//MB
Do đó: ABMD là hình bình hành
b: Ta có: ABMD là hình bình hành
=>AD=BM
mà AD=BC(ABCD là hình thang cân)
nên BM=BC
=>ΔBMC cân tại B
M
1
23 tháng 7 2023
Đặt A/B=C/D=k
=>A=k*B; C=D*k
A/B=k*B/B=k
\(\dfrac{A+C}{B+D}=\dfrac{k\cdot B+k\cdot D}{B+D}=k\)
=>\(\dfrac{A}{B}=\dfrac{A+C}{B+D}\)
CM
27 tháng 11 2017
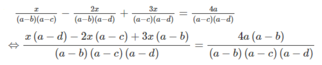
⇔ x(a − d) − 2x(a − c) + 3x(a − b) = 4a(a − b)
⇔ x(a − d − 2a + 2c + 3a − 3b) = 4a(a − b)
⇔ x(2a − 3b + 2c − d) = 4a(a − b)
Theo giả thiết, b + d = 2c nên 2a – 3b + 2c – d = 2a – 2b = 2 (a – b ).
Do đó phương trình đã cho tương đương với phương trình 2(a − b)x = 4a(a − b)
Để ý rằng a – b ≠ 0, ta thấy ngay phương trình cuối có nghiệm duy nhất x = 2a.
Vậy phương trình đã cho cũng có nghiệm duy nhất x = 2a.
12 tháng 4 2020
\(\frac{x}{\left(a-b\right)\left(a-c\right)}-\frac{2x}{\left(a-b\right)\left(a-d\right)}+\frac{3x}{\left(a-c\right)\left(a-d\right)}=\frac{4a}{\left(a-c\right)\left(a-d\right)}\)
\(\Leftrightarrow\frac{x\left(a-d\right)-2x\left(a-c\right)+3x\left(a-b\right)}{\left(a-b\right)\left(a-c\right)\left(a-d\right)}=\frac{4a\left(a-b\right)}{\left(a-b\right)\left(a-c\right)\left(a-d\right)}\)
\(\Leftrightarrow x\left(a-d-2a+2c+3a-3b\right)=4a\left(a-b\right)\)
\(\Leftrightarrow x\left(2a-3b+2c-d\right)=4a\left(a-b\right)\)
Theo giả thiết ,b + d = 2c nên 2a - 3b + 2c - d = 2a - 2b = 2(a-b) .Do đó phương trình đã cho tương đương với phương trình2(a-b) x = 4a(a-b)
Để ý rằng a - b \(\ne\)0,ta thấy ngay phương trình cuối có nghiệm duy nhất x = 2a
Vậy phương trình đã cho có nghiệm duy nhất x = 2a
c. ta có mẫu chung là 12 nên ta có phương trình tương đương
\(\frac{4\times\left(5x+4\right)}{12}-\frac{12}{12}=3\times\frac{\left(3x-2\right)}{12}\)
\(\Leftrightarrow20x+16-12=9x-6\)\(\Leftrightarrow11x=-10\Leftrightarrow x=-\frac{10}{11}\)
d. ta có \(PT\Leftrightarrow\frac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\frac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\frac{4x}{\left(x-1\right)\left(x+1\right)}\)
\(\Leftrightarrow\left(x+1\right)^2-\left(x-1\right)^2=4x\)
\(\Leftrightarrow4x=4x\) luôn đúng, vậy phương trình có nghiệm với mọi x
c, \(\Rightarrow20x+16-12=9x-6\Leftrightarrow11x=-10\Leftrightarrow x=-\dfrac{10}{11}\)
d, đk : x khác 1; -1
\(\Rightarrow x^2+2x+1-\left(x^2-2x+1\right)=4x\Leftrightarrow4x=4x\)
Vậy x\(\in\)R, xkhác 1 ; -1