Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
![]() và
và ![]() nên
nên ![]()
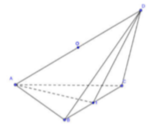
Pitago đảo dễ dàng suy ra tam giác ACD và tam giác ABD vuông có chung cạnh huyền AD.
Vậy tâm cầu ngoại tiếp tứ diện là trung điểm O của AD.

Chọn A.
![]() và
và ![]()
nên ![]()
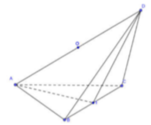
Pitago đảo dễ dàng suy ra tam giác ACD và tam giác ABD vuông có chung cạnh huyền AD.
Vậy tâm cầu ngoại tiếp tứ diện là trung điểm O của AD.

Đáp án A
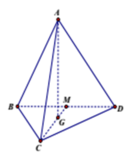
Gọi G là trọng tâm tam giác đều ABC suy ra G A ⊥ ( B C D )
Gọi M là trung điểm BD.
Đặt A C = x ⇒ G C = 2 3 C M = x 3 3
lại có A C 2 - G C 2 = A G 2
![]()
⇒ x = a 6 2
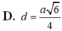
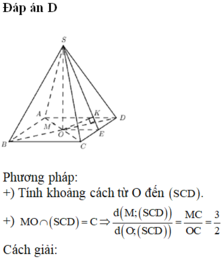


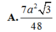
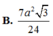
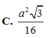
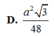


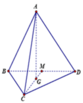

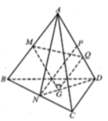
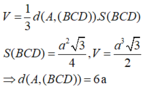


Lời giải:
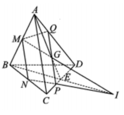
Vì $ABCD$ là tứ diện đều nên khoảng cách từ trọng tậm $O$ đến các mặt bên là như nhau:
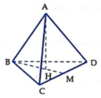
Lấy $H$ là trung điểm của $BC$, Vì tam giác $BCD$ đều nên
\(DH\perp BC\Rightarrow DH=\sqrt{BD^2-BH^2}=\sqrt{a^2-\frac{a^2}{4}}=\frac{\sqrt{3}}{2}a\)
\(\Rightarrow HO=\frac{1}{3}DH=\frac{\sqrt{3}}{6}a\)
\(AH=\sqrt{AB^2-BH^2}=\sqrt{a^2-\frac{a^2}{4}}=\frac{\sqrt{3}a}{2}\)
Do đó, \(AO=\sqrt{AH^2-HO^2}=\frac{\sqrt{6}a}{3}\)
\(\Rightarrow d(I,(BCD))=IO=\frac{AO}{2}=\frac{\sqrt{6}a}{6}\)
Kẻ \(OT\perp AH\Rightarrow d(O,(ABC))=OT=\sqrt{\frac{AO^2.HO^2}{AO^2+HO^2}}=\frac{\sqrt{6}a}{9}\)
\(\frac{d(I,(ABC))}{d(O,(ABC))}=\frac{AI}{IO}=\frac{1}{2}\Rightarrow d(I,(ABC))=\frac{\sqrt{6}a}{18}\)
Hay \(d(I,(ABC))=d(I,(ABD))=d(I,(ACD))=\frac{\sqrt{6}a}{18}\)