
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT giá trị tuyệt đối: \(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)
Ta có:\(M=\left(\left|-x+1\right|+\left|x-3\right|\right)+\left|x-2\right|\ge\left|-x+1+x-3\right|+\left|x-2\right|=2+\left|x-2\right|\ge2\) với mọi x
Do đó MMin=2
\(M=2\Leftrightarrow\int^{\left(-x+1\right).\left(x-3\right)\ge0}_{x=2}\Leftrightarrow\int^{1\le x\le3}_{x=2}\Leftrightarrow x=2\)
Vậy MMin=2 tại x=2

a)Vì \(|x-2|\ge0;\forall x\)
\(\Rightarrow|x-2|+5\ge0+5;\forall x\)
Hay \(A\ge5;\forall x\)
Dấu"="xảy ra \(\Leftrightarrow|x-2|=0\)
\(\Leftrightarrow x=2\)
Vậy \(A_{min}=5\)\(\Leftrightarrow x=2\)
b) Vì \(-|x+4|\le0;\forall x\)
\(\Rightarrow12-|x+4|\le12;\forall x\)
Hay \(B\le12;\forall x\)
Dấu"=" xayra \(\Leftrightarrow|x+4|=0\)
\(\Leftrightarrow x=-4\)
Vậy MAX \(B=12\)\(\Leftrightarrow x=-4\)
a, Ta có :
\(\left|x-2\right|\ge0\forall x\)
\(\Rightarrow\left|x-2\right|+5\ge5\forall x\)
Mà \(A=\left|x-2\right|+5\)
\(\Rightarrow A\ge5\forall x\)
\(\Rightarrow MinA=5\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)
Vậy \(MinA=5\Leftrightarrow x=2\)

GTNN nghĩa là giá trị nhỏ nhất đó bạn. Bạn biết thì giải giúp nhé

a: để Q(x)=0 thì (x-2)(x+2)=0
=>x=2 hoặc x=-2
b: \(Q\left(x\right)=x^2-4\ge-4\forall x\)
Dấu '=' xảy ra khi x=0

Ta có:
a) A = |x - 2| + |x - 4| + 2017|
=> A = |x - 2| + |4 - x| + 2017 \(\ge\)|x - 2 + 4 - x| + 2017 = |2| + 2017=2019
Dấu "=" xảy ra <=> (x - 2)(4 - x) \(\ge\)0
<=> 2 \(\le\)x \(\le\)4
Vậy MinA = 2019 <=> 2 \(\le\)x \(\)4
b) Ta có: B = |2019 - x| + |2020 - x|
=> B = |x - 2019| + |2020 - x| \(\ge\)|x - 2019 + 2020 - x| = |1| = 1
Dấu "=" xảy ra <=> (x - 2019)(2020 - x) \(\ge\)0
<=> 2019 \(\le\)x \(\le\)2020
Vậy MinB = 1 <=> 2019 \(\le\)x \(\le\)2020

2:
a: =-(x^2-12x-20)
=-(x^2-12x+36-56)
=-(x-6)^2+56<=56
Dấu = xảy ra khi x=6
b: =-(x^2+6x-7)
=-(x^2+6x+9-16)
=-(x+3)^2+16<=16
Dấu = xảy ra khi x=-3
c: =-(x^2-x-1)
=-(x^2-x+1/4-5/4)
=-(x-1/2)^2+5/4<=5/4
Dấu = xảy ra khi x=1/2
1)
a) \(A=x^2+4x+17\)
\(A=x^2+4x+4+13\)
\(A=\left(x+2\right)^2+13\)
Mà: \(\left(x+2\right)^2\ge0\) nên \(A=\left(x+2\right)^2+13\ge13\)
Dấu "=" xảy ra: \(\left(x+2\right)^2+13=13\Leftrightarrow x=-2\)
Vậy: \(A_{min}=13\) khi \(x=-2\)
b) \(B=x^2-8x+100\)
\(B=x^2-8x+16+84\)
\(B=\left(x-4\right)^2+84\)
Mà: \(\left(x-4\right)^2\ge0\) nên: \(A=\left(x-4\right)^2+84\ge84\)
Dấu "=" xảy ra: \(\left(x-4\right)^2+84=84\Leftrightarrow x=4\)
Vậy: \(B_{min}=84\) khi \(x=4\)
c) \(C=x^2+x+5\)
\(C=x^2+x+\dfrac{1}{4}+\dfrac{19}{4}\)
\(C=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}\)
Mà: \(\left(x+\dfrac{1}{2}\right)^2\ge0\) nên \(A=\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\)
Dấu "=" xảy ra: \(\left(x+\dfrac{1}{2}\right)^2+\dfrac{19}{4}=\dfrac{19}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
Vậy: \(A_{min}=\dfrac{19}{4}\) khi \(x=-\dfrac{1}{2}\)

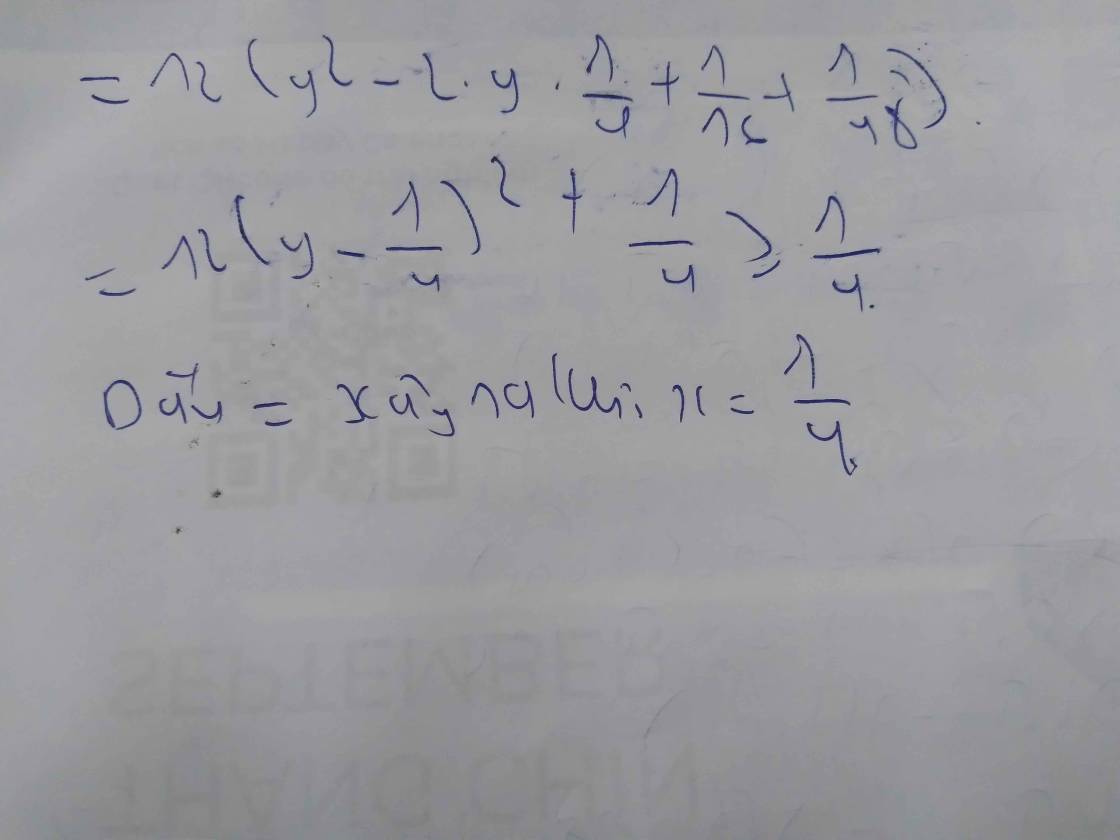

`A(x)=x^2-x-2`
`A(x)=x^2-2.x. 1/2+1/4-9/4`
`A(x)=(x-1/2)^2-9/4`
Vì `(x-1/2)^2 >= 0 AA x`
`=>(x-1/2)^2-9/4 >= -9/4 AA x`
Hay `A(x) >= -9/4 AA x`
Dấu "`=`" xảy ra `<=>(x-1/2)^2=0=>x-1/2=0=>x=1/2`
Vậy `GTN N` của `A(x)` là: `-9/4` khi `x=1/2`