Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

C5:
hàm số cắt trục tung tại điểm A(0;a)=> thay A vào hàm số suy ra a=5 => B
C6:
hàm số cắt trục hoành tại điểm B(b;0) => thay B vào hàm số suy ra b=3/2 => A
C7:
hàm số đi qua A(1;-3)=> thay A vào hàm số ta được m=0 => A

\(B=\frac{\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)}{3+\sqrt{5}}=3-\sqrt{5}\)
\(C=\frac{1}{\sqrt{5}+\sqrt{3}}-\frac{1}{\sqrt{5}-\sqrt{3}}\)
\(=\frac{\sqrt{5}-\sqrt{3}}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}-\frac{\sqrt{5}+\sqrt{3}}{\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}+\sqrt{3}\right)}\)
\(=\frac{\sqrt{5}-\sqrt{3}-\sqrt{5}-\sqrt{3}}{2}\)
\(=\frac{-2\sqrt{3}}{2}=-\sqrt{3}\)
\(D=\frac{2}{\sqrt{3}+1}+\frac{1}{\sqrt{3}-2}+\frac{6}{\sqrt{3}+3}\)
\(=\frac{2\left(\sqrt{3}-1\right)}{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}+\frac{\sqrt{3}+2}{\left(\sqrt{3}-2\right)\left(\sqrt{3}+2\right)}+\frac{6\left(3-\sqrt{3}\right)}{\left(\sqrt{3}+3\right)\left(3-\sqrt{3}\right)}\)
\(=\sqrt{3}-1-\left(\sqrt{3}+2\right)-\left(3-\sqrt{3}\right)\)
\(=\sqrt{3}-1-\sqrt{3}-2-3+\sqrt{3}=\sqrt{3}-6\)

a) \(\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{\sqrt{5}-5}{1-\sqrt{5}}\right):\dfrac{1}{\sqrt{2}-\sqrt{5}}\)
\(=\left[-\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}-\dfrac{\sqrt{5}\left(1-\sqrt{5}\right)}{1-\sqrt{5}}\right]\cdot\left(\sqrt{2}-\sqrt{5}\right)\)
\(=\left(-\sqrt{2}-\sqrt{5}\right)\left(\sqrt{2}-\sqrt{5}\right)\)
\(=-\left(\sqrt{2}+\sqrt{5}\right)\left(\sqrt{2}-\sqrt{5}\right)\)
\(=-\left(2-5\right)\)
\(=-\left(-3\right)\)
\(=3\)
b) Ta có:
\(x^2-x\sqrt{3}+1\)
\(=x^2-2\cdot\dfrac{\sqrt{3}}{2}\cdot x+\left(\dfrac{\sqrt{3}}{2}\right)^2+\dfrac{1}{4}\)
\(=\left(x-\dfrac{\sqrt{3}}{2}\right)^2+\dfrac{1}{4}\)
Mà: \(\left(x-\dfrac{\sqrt{3}}{2}\right)^2\ge0\forall x\) nên
\(\left(x-\dfrac{\sqrt{3}}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\forall x\)
Dấu "=" xảy ra:
\(\left(x-\dfrac{\sqrt{3}}{2}\right)^2+\dfrac{1}{4}=\dfrac{1}{4}\)
\(\Leftrightarrow x=\dfrac{\sqrt{3}}{2}\)
Vậy: GTNN của biểu thức là \(\dfrac{1}{4}\) tại \(x=\dfrac{\sqrt{3}}{2}\)
a)
\(\left(\dfrac{\sqrt{6}-\sqrt{2}}{1-\sqrt{3}}-\dfrac{\sqrt{5}-5}{1-\sqrt{5}}\right):\dfrac{1}{\sqrt{2}-\sqrt{5}}\\ =\left(-\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}-\dfrac{\sqrt{5}\left(1-\sqrt{5}\right)}{1-\sqrt{5}}\right).\left(\sqrt{2}-\sqrt{5}\right)\\ =\left(-\sqrt{2}-\sqrt{5}\right).\left(\sqrt{2}-\sqrt{5}\right)\\ =-\left(\sqrt{2}+\sqrt{5}\right)\left(\sqrt{2}-\sqrt{5}\right)\\ =-\left(\sqrt{2}^2-\sqrt{5}^2\right)\\ =-\left(2-5\right)\\ =-\left(-3\right)\\ =3\)

Bài 1:
Để M có nghĩa thì \(\left\{{}\begin{matrix}x+4\ge0\\2-x\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-4\\x\le2\end{matrix}\right.\Leftrightarrow-4\le x\le2\)
Số giá trị nguyên thỏa mãn điều kiện là:
\(\left(2+4\right)+1=7\)

ai nay dung kinh nghiem la chinh
cau a)
ta thay \(10+6\sqrt{3}=\left(1+\sqrt{3}\right)^3\)
\(6+2\sqrt{5}=\left(1+\sqrt{5}\right)^2\)
khi do \(x=\frac{\sqrt[3]{\left(\sqrt{3}+1\right)^3}\left(\sqrt{3}-1\right)}{\sqrt{\left(1+\sqrt{5}\right)^2}-\sqrt{5}}\)
\(x=\frac{\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}{1+\sqrt{5}-\sqrt{5}}\)
\(x=\frac{3-1}{1}=2\)
suy ra
x^3-4x+1=1
A=1^2018
A=1
b)
ta thay
\(7+5\sqrt{2}=\left(1+\sqrt{2}\right)^3\)
khi do
\(x=\sqrt[3]{\left(1+\sqrt{2}\right)^3}-\frac{1}{\sqrt[3]{\left(1+\sqrt{2}\right)^3}}\)
\(x=1+\sqrt{2}-\frac{1}{1+\sqrt{2}}=\frac{\left(1+\sqrt{2}\right)^2-1}{1+\sqrt{2}}=\frac{2+2\sqrt{2}}{1+\sqrt{2}}\)
x=2
thay vao
x^3+3x-14=0
B=0^2018
B=0
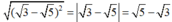
Chọn đáp án A