Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(M=\frac{x}{xy+x+2015}+\frac{y}{yz+y+1}+\frac{2015z}{xz+2015z+2015}\)
\(\Leftrightarrow M=\frac{x}{xy+x+xyz}+\frac{y}{yz+y+1}+\frac{xyz.z}{xz+xyz.z+xyz}\left(xyz=2015\right)\)
\(\Leftrightarrow M=\frac{1}{y+1+yz}+\frac{y}{yz+y+1}+\frac{yz}{1+yz+y}\)
\(\Leftrightarrow M=\frac{yz+y+1}{yz+y+1}=1\)
\(M=\frac{x}{xy+x+2015}+\frac{y}{yz+y+1}+\frac{2015z}{xz+2015z+2015}\)
Thay xyz = 2015, Ta có:
\(M=\frac{x}{xy+x+xyz}+\frac{y}{yz+y+1}+\frac{xyz^2}{xz+xyz^2+xyz}\)
\(M=\frac{1}{y+1+yz}+\frac{y}{yz+y+1}+\frac{yz}{1+yz+y}\)
\(M=\frac{y+1+yz}{y+1+yz}=1\)

M = x 3 + y 3 + z 3 - 3 x y z x 2 + y 2 + z 2 - x y - y z - x z
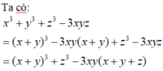
![]()
![]()
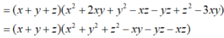
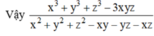
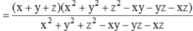
![]()


\(\frac{xy+2x+1}{xy+x+y+1}+\frac{yz+2y+1}{yz+y+z+1}+\frac{zx+2z+1}{zx+z+x+1}\)
Ta có: \(\frac{xy+2x+1}{xy+x+y+1}=\frac{\left(xy+x\right)+\left(x+1\right)}{\left(xy+x\right)+\left(y+1\right)}=\frac{x\left(y+1\right)+\left(x+1\right)}{\left(y+1\right)\left(x+1\right)}=\frac{x}{x+1}+\frac{1}{y+1}\)
Tương tự ta có:
\(\frac{yz+2y+1}{yz+y+z+1}=\frac{y}{y+1}+\frac{1}{z+1}\)
\(\frac{zx+2z+1}{zx+z+x+1}=\frac{z}{z+1}+\frac{1}{x+1}\)
Từ đây ta có biểu thức ban đầu sẽ bằng
\(\frac{x}{x+1}+\frac{1}{y+1}+\frac{y}{y+1}+\frac{1}{z+1}+\frac{z}{z+1}+\frac{1}{x+1}\)
\(\left(\frac{x}{x+1}+\frac{1}{x+1}\right)+\left(\frac{y}{y+1}+\frac{1}{y+1}\right)+\left(\frac{z}{z+1}+\frac{1}{z+1}\right)=1+1+1=3\)
CHÚ Ý: ab+a+b+1=a(b+1)+(b+1)=(a+1)(b+1)
Xét: \(\frac{xy+2x+1}{xy+x+y+1}=\frac{x\left(y+1\right)+x+1}{\left(x+1\right)\left(y+1\right)}=\frac{x}{x+1}+\frac{1}{y+1}\)
Tương tự với 2 biểu thức còn lại ta được:
A=\(\frac{x}{x+1}+\frac{1}{y+1}+\frac{y}{y+1}+\frac{1}{z+1}+\frac{z}{z+1}+\frac{1}{x+1}\)
=\(\frac{x+1}{x+1}+\frac{y+1}{y+1}+\frac{z+1}{z+1}=1+1+1=3\)

???
?????????????////////////////////////////////////
mik có cách giải rồi
xy+yz+xz>=\(3\sqrt[3]{xyz^2}\) mà xyz=1
suy ra xy+yz+xz>=3 mà xy+yz+xz=3
suy ra 3=3 suy ra dấu "=" xảy ra suy ra x=y=z
A=3x/3x3=1/x2
b, x.y2.z3=64 mà x=y=z
nên x6=64 suy ra x=2
thay x=2 vào A=3x/3x3=1/x2
A=1/4