Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số thứ nhất là a; số thứ hai là b
Ta có 1/3*a-b=1
=> 1/3*a=b+1
=> a=(b+1):1/3
=> a=(b+1)*3
Mà a+b=43
Hay (b+1)*3+b=43
<=> 3b+3+b=43
<=> 4b+3=43
<=> 4b=43-3
<=> 4b=40
=> b=40:4
=> b=10
=>a=(10+1)*3
=>a=11*3
=>a=33
Vậy số thứ nhất là 33;số thứ 2 là 10

Bài 1:
\(c,\text{PT có 2 }n_0\text{ phân biệt }\Leftrightarrow\Delta'=2^2-2m>0\Leftrightarrow2m< 4\Leftrightarrow m< 2\)

a) Xét: x2 - 4mx + 9.(m – 1)2 = 0 (1)
Δ’ = (2.m)2 – 9.(m – 1)2 = 4m2 – 9.(m2 – 2m + 1) = -5m2 + 18m – 9
Phương trình (1) có nghiệm ⇔ Δ’ ≥ 0
⇔ -5m2 + 18m – 9 ≥ 0
⇔ 5m2 - 18m + 9 ≤ 0
⇔ (5m – 3)(m – 3) ≤ 0
⇔ 3/5 ≤ m ≤ 3.
b) + x1 ; x2 là hai nghiệm của (1) nên theo định lý Vi-et ta có:
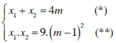
+ Tìm hệ thức giữa x1 và x2 không phụ thuộc vào m.
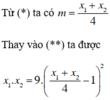
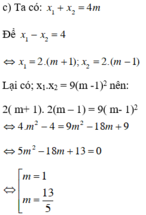
Thử lại:
+ m = 1, (1) trở thành x2 – 4x = 0 có hai nghiệm x = 0; x = 4 có hiệu bằng 4
+ m = 13/5, (1) trở thành 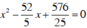 có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
có hai nghiệm x = 7,2 và x = 3,2 có hiệu bằng 4.
Vậy m = 1 hoặc m = 13/5.

Gọi a là chữ số hàng chục, b là chữ số hàng đơn vị. Điều kiện a, b nguyên 1 ≤ a ≤ 9 và 0 ≤ b ≤ 9. Ta có:
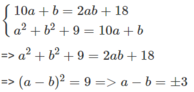 '
'
Trường hợp 1
a - b = 3 ⇒ a = b + 3
Thay vào phương trình đầu của hệ phương trình ta được:
11b + 30 = 2(b + 3)b + 18 ⇒ 2 b 2 - 5 b + 12 = 0
Phương trình cuối có hai nghiệm: b 1 = 4 , b 2 = -3/2
Giá trị b 2 = -3/2 không thỏa mãn điều kiện 0 ≤ b ≤ 9 nên nên bị loại.
Vậy b = 4, suy ra a = 7.
Trường hợp 2
a - b = - 3 ⇒ a = b - 3
Thay vào phương trình của hệ phương trình ra được
11b - 30 = 2(b - 3)b + 18 ⇒ 2 b 2 - 17 b + 48 = 0
Phương trình này vô nghiệm.
Vậy số phải tìm là 74.

a) An: "\(\forall x \in \mathbb R ,{x^2} \ge 0\)"
b) Bình: "\(\exists x \in ,{x^2} < 0\)"
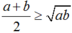
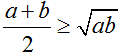
Gọi 2 số đó là a và b (a\(\ge0,b\ge0\) )
câu a
Áp dụng BĐT Bu-nhia -xkop-ki ,ta có
a+b\(\le\sqrt{\left(a^2+b^2\right)\left(1^2+1^2\right)}\)
\(\Leftrightarrow82\le\sqrt{\left(a^2+b^2\right)2}\) \(\Rightarrow\) \(6724\le\left(a^2+b^2\right)2\Leftrightarrow\left(a^2+b^2\right)\ge3362\)
Vậy Min a2+b2=3362\(\Leftrightarrow a=b=41\)