Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
x 3 - 3 x 2 + 2 x - 1 = x 2 - 3 x + 1 ⇔ x 3 - 4 x 2 + 5 x - 2 = 0 ⇔ [ x = 1 x = 2
Tọa độ giao điểm A(1;-1), B(2;-1)
⇒ A B = 1 2 + 0 2 = 1
Chọn đáp án C.

Đáp án C
Phương pháp:
+) Giải phương trình hoành độ giao điểm của hai đồ thị hàm số. Tìm tọa độ điểm A, B.
+) Tính độ dài đoạn thẳng AB.
Cách giải:
Phương trình hoành độ giao điểm của hai đồ thị hàm số là:
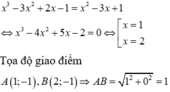

Đáp án A
PT hoành độ giao điểm là x + 1 = x + 3 x − 1 ⇔ x ≠ 1 x 2 − x − 4 = 0 , Δ = 17 > 0 ⇒ x A + x B = 1 y A + y B = − 4
Suy ra A x A ; x A + 1 B x B ; x B + 1 ⇒ A B = 2 x A − x B 2 = 2 x A + x B 2 − 8 x A x B = 2 1 2 − 8 − 4 = 34

Đáp án C
PT hoành độ giao điểm: 2 x − 1 x + 1 = x − 1
⇔ x ≠ − 1 x 2 − 2 x = 0 ⇔ x = 0 x = ⇒ A 0 ; − 1 B 2 ; 1 ⇒ A B = 2 2 .

Đáp án D
Phương trình hoành độ giao điểm là:
x 3 − 3 x 2 + 2 x − 1 = x 2 − 3 x + 1
⇔ x 3 − 4 x 2 + 5 x − 2 = 0 ⇔ x − 2 x − 1 2 = 0
⇔ x = 1 ⇒ y = − 1 x = 2 ⇒ y = − 1 ⇒ A B = 1

Đáp án B
Phương trình hoành độ giao điểm là:
x − 3 x − 1 = 1 − x ⇔ x ≠ 1 x − 3 = − x 2 + 2 x − 1 ⇔ x ≠ 1 x 2 − x − 2 = 0
⇔ x = − 1 ⇒ y = 2 x = 2 ⇒ y = − 1 ⇒ A − 1 ; 2 ; B 2 ; − 1 ⇒ A B = 3 2

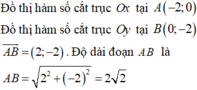

Chọn D.
Giải phương trình hoành độ giao điểm của đồ thị hàm số đã cho với đường thẳng y = 1 để xác định tọa độ
điểm A và B . Sau đó tính độ dài đoạn thẳng
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho với đường thẳng y = 1 là: