Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lấy số dương ε bé tùy ý bất kì:
⇒ có một số n0 thỏa mãn: |vn| < ε kể từ n = n0.
⇒ |un – 2| < vn < |vn| < ε kể từ n = n0 trở đi
⇒ lim (un – 2) = 0
⇒ lim un = 2.

Dãy ( u n + v n ) không có giới hạn hữu hạn.
Thật vậy, giả sử ngược lại ( u n + v n ) có giới hạn hữu hạn.
Khi đó, các dãy số ( u n + v n ) v à ( u n ) cùng có giới hạn hữu hạn, nên hiệu của chúng cũng là một dãy có giới hạn hữu hạn, nghĩa là dãy số có số hạng tổng quát là u n + v n − u n = v n có giới hạn hữu hạn. Điều này trái với giả thiết ( v n ) không có giới hạn hữu hạn.

1/ \(\lim\limits\dfrac{\dfrac{2^n}{7^n}-5.7.\left(\dfrac{7}{7}\right)^n}{\dfrac{2^n}{7^n}+\left(\dfrac{7}{7}\right)^n}=-35\)
2/ \(\lim\limits\dfrac{\dfrac{3^n}{7^n}-2.5.\left(\dfrac{5}{7}\right)^n}{\dfrac{2^n}{7^n}+\dfrac{7^n}{7^n}}=0\)
3/ \(\lim\limits\sqrt[3]{\dfrac{\dfrac{5}{n}-\dfrac{8n}{n}}{\dfrac{n}{n}+\dfrac{3}{n}}}=\sqrt[3]{-8}=-2\)

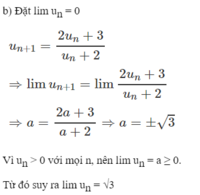
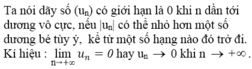
Vì ( u n ) có giới hạn là 0 nên | u n | có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Mặt khác, | v n | = | | u n | | = | u n | . Do đó, | v n | cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi. Vậy ( v n ) có giới hạn là 0.