Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng với mỗi nguồn, đo khoảng cách \(x_1,x_2\). Tính \(\dfrac{x_1-x_2}{\lambda}\) với \(\lambda\) được xác định trong câu hỏi trước. Nếu thương số nhận được là một số nguyên thì kết quả đúng với công thức.

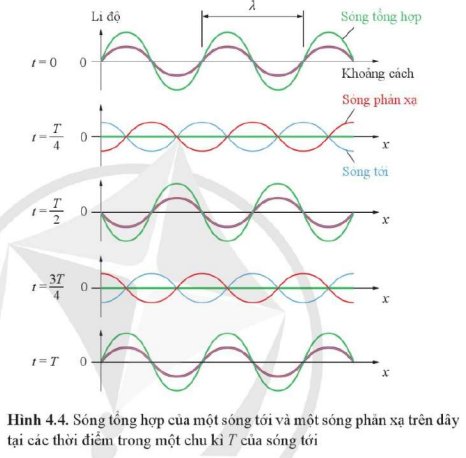
Vị trí các nút là những điểm không dao động.
- Khoảng cách giữa hai nút sóng liên tiếp bằng nửa bước sóng.
https://khoahoc.vietjack.com/question/1205183/hay-chi-ra-vi-tri-cac-nut-song-tren-hinh-44-xac-dinh-khoang-cach-giua-hai-nut-song-lien-tiep
=> Tôi xin bạn, tôi cầu bạn, tôi lạy bạn, tôi vái bạn trăm vái rồi bạn đừng copy nữa được không? :( copy mà cũng ăn được GP thì tôi cũng không hiểu :D

\(MA=6cm;MB=AB-MA=20-6=14cm\)
\(AM\perp MC\Rightarrow AC=\sqrt{AM^2+MC^2}=\sqrt{6^2+8^2}=10cm\)
\(BM\perp MC\Rightarrow BC=\sqrt{BM^2+MC^2}=\sqrt{14^2+8^2}=2\sqrt{65}cm\)
Xét một điểm N bất kì trên CM ta có: \(d_2-d_1=k\lambda\)
Hai nguồn dao động cùng pha:
\(\Rightarrow\left\{{}\begin{matrix}d_2-d_1=\left(k+0,5\right)\lambda\\BC-AC\le k\lambda\le BM-AM\end{matrix}\right.\)
\(\Rightarrow2\sqrt{65}-10\le k+0,5\le14-6\Rightarrow5,62\le k\le7,5\)
\(\Rightarrow k=\left\{6,5;7,5\right\}\)
Vậy có hai điểm cực tiểu trên CD.

a) Vì hai điểm gần nhất trên cùng phương truyền sóng dao động lệch pha nhau một góc \(\dfrac{\pi}{2}\)
Khoảng cách giữa hai điểm là 360cm= \(\dfrac{3\lambda}{2}\) nên hai điểm này dao động ngược pha nhau độ lệch pha của chúng là π
b) Sau 0,1s sóng truyền được khoảng cách là 0,1.330 = 33m = \(\dfrac{55\lambda}{4}\)
Độ lệch pha là \(\dfrac{3\pi}{4}\)

Khoảng cách giữa 9 vân sáng liên tiếp là 25,3 mm :
\(8i=25,3\Leftrightarrow i=3,1625mm=3,1625.10^{-3}m\)
\(a=0,2mm=2.10^{-4}m\)
\(D=1m\)
\(a,\) Bước sóng : \(i=\dfrac{\lambda D}{a}\Leftrightarrow\lambda=\dfrac{ia}{D}=\dfrac{3,1625.10^{-3}.2.10^{-4}}{1}=6,325.10^{-7}\left(m\right)\)
\(b,\) Vân sáng bậc hai : \(x_{S2}=2i=2.3,1625.10^{-3}=6,325.10^{-3}\left(m\right)\)
Vân tối thứ tư : \(x_{T4}=\left(3+\dfrac{1}{2}\right)i=\dfrac{7}{2}.3,1625.10^{-3}=0,011\left(m\right)\)
Khoảng cách từ vân sáng bậc hai đến vẫn tối thứ tư ở cùng bên so với vân sáng trung tâm là :
\(d=\left|x_{T4}-x_{S2}\right|=\left|0,011-6,325.10^{-3}\right|=4,675.10^{-3}\left(m\right)\)
Vậy ...

a) Khoảng vân của ánh sáng có bước sóng là 400 nm: \({i_1} = \frac{{{\lambda _1}D}}{a} = \frac{{400.1,5}}{{0,2}} = 3mm\)
⇒Vân sáng bậc ba cùng phía với vân trung tâm nằm ở vị trí 3i1=3.3=9mm
Khoảng vân của ánh sáng có bước sóng là 600 nm: \({i_2} = \frac{{{\lambda _2}D}}{a} = \frac{{600.1,5}}{{0,2}} = 4,5mm\)
⇒Vân sáng bậc ba cùng phía với vân trung tâm nằm ở vị trí 3i2=3.4,5=13,5mm
Khoảng cách giữa hai vân sáng bậc ba cùng phía với vân trung tâm là: 13,5-9=4,5 mm
b) ánh sáng đơn sắc có bước sóng là 400 nm nằm trong khoảng ánh sáng màu tím (380-435 nm)và ánh sáng có bước sóng 600 nm nằm trong khoảng ánh sáng màu cam (590-625 nm) trộn hia ánh sáng này lại với nhau ta sẽ thu được ánh sáng trắng.
Ta có: \(\frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{{400}}{{600}} = \frac{2}{3}\) ⇒3λ1=2λ2
Vân sáng thứ 3 của ánh sáng thứ nhất trùng với vân sáng thứ 2 của ánh sáng thứ hai nên khoảng cách là 9mm

Ta có: \(u=Acos\left(\dfrac{2\pi}{T}t-\dfrac{2\pi x}{\lambda}\right)\)
Khoảng cách giữa hai điểm gần nhau nhất dao động cùng pha là λ và khoảng cách giữa hai điểm gần nhau nhất dao động ngược pha là \(\dfrac{\lambda}{2}\)

Phao cầu cá nhỏ lên cao 6 lần trong 4 s tương ứng với 5T nên ta có T = 0,8 s
Khoảng cách giữa hai đỉnh sóng liên tiếp là: λ = v.T = 0,5.0,8 = 0,4m
Tham khảo:
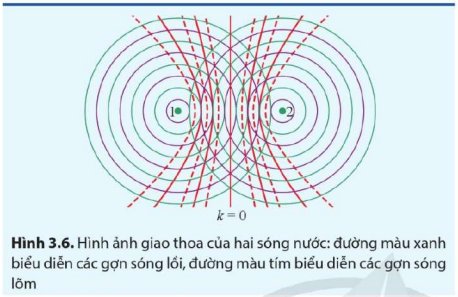
- Cách xác định bước sóng do hai nguồn phát ra:
+ Đo khoảng cách giữa hai nguồn.
+ Đếm số khoảng cách giữa đỉnh hai gợn lồi liên tiếp hoặc số khoảng cách giữa đỉnh hai gợn lõm liên tiếp do hai nguồn tạo ra.
+ Dựa vào khái niệm bước sóng là khoảng cách gần nhau nhất giữa hai gợn lồi hoặc hai gợn lõm.
- Áp dụng:
+ Giả sử đối với hình 3.6 ở trên ta đo được khoảng cách giữa hai nguồn S1S2 = a
+ Khoảng giữa hai nguồn có 4 gợn lồi (không tính 2 nguồn) bằng 3.
Khi đó hoàn toàn tính được bước sóng \(\lambda=\dfrac{a}{3}\)